平面図形の問題が苦手です[中学受験]
お気に入りに登録
平山入試研究所の小泉浩明さんが、中学受験・志望校合格を目指す親子にアドバイスする実践的なコーナーです。保護者のかたから寄せられた疑問に小泉さんが回答します。


質問者
小5女子のお母様質問
平面図形の問題が苦手です。立体図形もあまり得意ではないですが、まだマシです。イメージをして、上手く補助線を引く作業ができません。幼児期にブロックや積み木、折り紙は好まず、あまり遊ばなかったのが影響しているのでしょうか? これから力を付けていくにはどうしたら良いでしょう?小泉先生のアドバイス
【図形問題の解き方】を意識し、問題演習を重ねる
女の子で立体図形が苦手なお子さまは多いのですが、お母さんが指摘されるように、「幼児期にブロックや積み木、折り紙は好まず」、その結果として平面図形や立体図形が苦手になった可能性はあるかもしれません。ただし、今からブロック遊びをする時間もありませんから、いくつかの点に注意しながら、問題演習を重ねることが一番の得策だと考えます。
図形問題の解き方の流れは、一般的に以下のようになります。
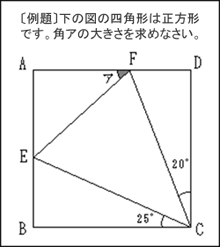 それでは、右の例題を使って説明していきましょう。
それでは、右の例題を使って説明していきましょう。
まず、「(1)問題文にある条件はすべて図に書き込む」
ですが、問題文にあって、図にはまだ記されていない
下記の条件を図に書き込みます。
BC=CD(=AD=AB)
角EBC、角BCD、角FDC、角EAFは直角
また「(2)簡単な計算で出る条件はすべて図に書き込む」ですが、たとえば角BCDは90(度)ですから、角ECFは45(度)になります。
これらの条件を図に書き込むと、右下の図1になります。
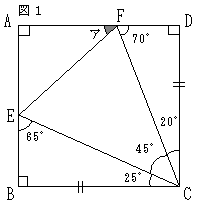 この図を見ながら解法を探っていくのですが、実は、ここまでの作業を「やらない」あるいは「やれない」お子さまが実に多いようです。特に図形が苦手な生徒は、問題文と図形を交互に「ながめる」だけで、ほとんど手を動かそうとしないのが特徴です。
この図を見ながら解法を探っていくのですが、実は、ここまでの作業を「やらない」あるいは「やれない」お子さまが実に多いようです。特に図形が苦手な生徒は、問題文と図形を交互に「ながめる」だけで、ほとんど手を動かそうとしないのが特徴です。
一度、図形問題を解くお子さまの様子をじっくりご覧になってください。そして図形問題の前で、呆然としているようであれば、「手を動かしてごらん」とか、「わかる条件を図に入れてみなさい」などのアドバイスを与えてあげると良いと思います。
さて、書き込めるだけの条件をすべて図に書いたら、次はその図をじっくり見て、解法をさぐっていきます。ここで大切なのは、いくつかの点に注目することです。
すなわち、
i)「同じところ」に注目
ii)「特別なところ」に注目
iii)「図形の移動・補助線」に注目
ということです。
「同じところ」や「特別なところ」に注目するのは、それにより「図形の性質」や「相似・合同」などを使い、答えを得たいからです。
また「図形の移動・補助線」に注目するのは、そのままでは答えを得られないので、答えを得るための突破口を開こうとしているのです。お子さまも、この「補助線」が苦手ということですが補助線をうまく使えるようになったら、図形問題はかなり上達していると言って良いでしょう。
補助線の使い方はある程度は決まっているようですが(例:「平行を作るように引く」など)、かといってそれですべての問題が解けるわけではありません。やはり多くの問題を解いてさまざまな経験を積むことで、「図形の移動」や「補助線」の使い方がうまくなり、結果として問題が解けるようになるということなのです。その意味では、お子さまの図形問題の苦手を克服するには、たくさんの問題を解くことは必要なプロセスと言えるでしょう。
ただし、漫然と解くのではなく、【図形問題の解き方】のステップを踏みながら、注意深く問題を解いていくことが必要です。お子さまの性格は、「おおざっぱなところがある」ということですから、条件を書き込んだ図形に集中するようなクセを付けたいものです。
※解き方としては、三角形ECFの中に三角形BCE、三角形DCFをそれぞれ直線CE、CFで折り返す方法もありますが、基本的には同じ考え方です。
女の子で立体図形が苦手なお子さまは多いのですが、お母さんが指摘されるように、「幼児期にブロックや積み木、折り紙は好まず」、その結果として平面図形や立体図形が苦手になった可能性はあるかもしれません。ただし、今からブロック遊びをする時間もありませんから、いくつかの点に注意しながら、問題演習を重ねることが一番の得策だと考えます。
図形問題の解き方の流れは、一般的に以下のようになります。
【図形問題の解き方】
(1)問題文にある条件はすべて図に書き込む。
(2)簡単な計算で出る条件はすべて図に書き込む。
(4)「図形の性質」「相似」「合同」「面積比」などを使って答えを得る。
(1)問題文にある条件はすべて図に書き込む。
(2)簡単な計算で出る条件はすべて図に書き込む。
| (3)図で考える | i)「同じところ」に注目 |
| ii)「特別なところ」に注目 | |
| iii)「図形の移動・補助線」に注目 |
 それでは、右の例題を使って説明していきましょう。
それでは、右の例題を使って説明していきましょう。まず、「(1)問題文にある条件はすべて図に書き込む」
ですが、問題文にあって、図にはまだ記されていない
下記の条件を図に書き込みます。
BC=CD(=AD=AB)
角EBC、角BCD、角FDC、角EAFは直角
また「(2)簡単な計算で出る条件はすべて図に書き込む」ですが、たとえば角BCDは90(度)ですから、角ECFは45(度)になります。
これらの条件を図に書き込むと、右下の図1になります。
 この図を見ながら解法を探っていくのですが、実は、ここまでの作業を「やらない」あるいは「やれない」お子さまが実に多いようです。特に図形が苦手な生徒は、問題文と図形を交互に「ながめる」だけで、ほとんど手を動かそうとしないのが特徴です。
この図を見ながら解法を探っていくのですが、実は、ここまでの作業を「やらない」あるいは「やれない」お子さまが実に多いようです。特に図形が苦手な生徒は、問題文と図形を交互に「ながめる」だけで、ほとんど手を動かそうとしないのが特徴です。一度、図形問題を解くお子さまの様子をじっくりご覧になってください。そして図形問題の前で、呆然としているようであれば、「手を動かしてごらん」とか、「わかる条件を図に入れてみなさい」などのアドバイスを与えてあげると良いと思います。
さて、書き込めるだけの条件をすべて図に書いたら、次はその図をじっくり見て、解法をさぐっていきます。ここで大切なのは、いくつかの点に注目することです。
すなわち、
i)「同じところ」に注目
ii)「特別なところ」に注目
iii)「図形の移動・補助線」に注目
ということです。
「同じところ」や「特別なところ」に注目するのは、それにより「図形の性質」や「相似・合同」などを使い、答えを得たいからです。
また「図形の移動・補助線」に注目するのは、そのままでは答えを得られないので、答えを得るための突破口を開こうとしているのです。お子さまも、この「補助線」が苦手ということですが補助線をうまく使えるようになったら、図形問題はかなり上達していると言って良いでしょう。
補助線の使い方はある程度は決まっているようですが(例:「平行を作るように引く」など)、かといってそれですべての問題が解けるわけではありません。やはり多くの問題を解いてさまざまな経験を積むことで、「図形の移動」や「補助線」の使い方がうまくなり、結果として問題が解けるようになるということなのです。その意味では、お子さまの図形問題の苦手を克服するには、たくさんの問題を解くことは必要なプロセスと言えるでしょう。
ただし、漫然と解くのではなく、【図形問題の解き方】のステップを踏みながら、注意深く問題を解いていくことが必要です。お子さまの性格は、「おおざっぱなところがある」ということですから、条件を書き込んだ図形に集中するようなクセを付けたいものです。
| 解法の説明を続けます。 ここで図1に集中すると、同じところがいくつも見つかります。たとえば角ECFは45(度)であり、角BCEと角DCFを合わせたものも45(度)で同じです。そしてそれにより、「ひょっとしたら、三角形ECFは三角形BCEと三角形DCFを合わせたものと同じ(合同)ではないか(同じだったらうまい!)」という発想が出てきます。そして図形を移動させることで(図2)、見事に答えを得るための突破口が開けました(図3)。 図3において三角形ECFと三角形GCFは、「2辺とその間の角が等しい」ため合同であり、角CFEは角CFDと同じく70(度)になります。よって角アは180!)70×2=40(度)であることがわかります。以上がこの問題の解き方ですが、図形の移動をうまく使って解く問題でした。 問題演習を重ねることは、「図形の移動・補助線」の使い方を上達させる確かな方法だと思います。ただしくり返し言いますが、「問題文にある条件はすべて図に書き込む」「簡単な計算で出る条件はすべて図に書き込む」「図で考える」などの【図形問題の解き方】を意識し、実際に手を動かすことにより、より早い上達が可能になると考えます。 |  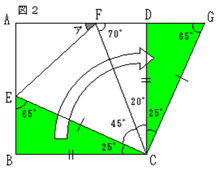 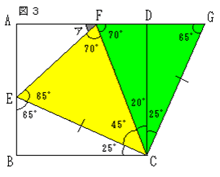 |
※解き方としては、三角形ECFの中に三角形BCE、三角形DCFをそれぞれ直線CE、CFで折り返す方法もありますが、基本的には同じ考え方です。















![算数「速さと比(1)」[中学受験]](http://benesse.jp/common/static/kj/common/images/chu/432/080610_q1_1.gif)









