算数の苦手、どう克服する？ [中学受験　5年生]

5年生の秋になると、学習内容が難しくなるうえ、比と割合、速さ・旅人算など、苦手になりやすい単元が出てきます。カリキュラムのスピードが上がることも多く、理解が不十分な単元が増え、慢性的な苦手に陥るケースもあります。そこで今回は、算数を苦手にしないために、これだけはおさえておきたいポイントについてお話しします。

学習は、例題レベルに絞ってOK

算数は、得意な子とそうでない子との差がつきやすい教科です。塾に通っている場合、学ぶべき単元の量が多いため、不得意な子にはついていけないスピードで授業が進んでしまう場合があります。理解に時間がかかるのは、決して悪いことではありません。問題は、理解が不十分なまま「なんとなく」問題を解く癖がついてしまうことです。

ですから、お子さまが「算数は苦手かな」と感じたら、テキストの例題レベルの問題に絞り、人に説明できるくらいしっかり理解できている状態をめざしてください。例題は、その単元の基礎です。応用問題は基礎の組み合わせですから、基礎ができれば、少しずつできるようになっていきます。「応用問題は、今はできなくてもOK」とお子さまにはっきり言ってあげてかまいません。

苦手な一行問題を、対話しながら一緒に解く

全ての単元を保護者のかたが教える必要はありませんが、理解があいまいだと感じられる例題があれば、お子さまと対話しながら、ぜひ一緒に考えてみてください。
例えば、以下のような「つるかめ算」の問題。

つるとかめが合計10います。足の数は合計28本です。つるは何羽、かめは何匹いますか。

かめの足は4本、つるの足は2本。このように、2種類の数が出てくる場合「どちらか一方だけだったら」と仮定するのが、基本となる考え方です。
全部がかめだったら、足の数は？……　4本×10匹＝40本
全部がつるだったら、足の数は？……　2本×10羽＝20本

では、かめの中に、つるが一羽まざっていたら？　足は38本になりますね。
つるの中に、かめが一匹、まざっていたとしたら？　足は22本です。
つまり、一羽（匹）まざるごとに、2本の差が出るわけです。

40本－28本＝12本　
全部かめの場合より、足が12本少ないということは、
12÷2＝6　6羽のつるがまざっていることになります。

28本－20本＝8本
全部つるの場合より、足が8本多いということは、
8÷2＝4　4匹のかめがまざっていることになります。

「どちらか一方だけだったらと仮定する」考え方は、和差算や平均の問題にも使えます。
なお、塾では、合計の「10」を横軸、「2本」と「4本」を縦軸においた面積図で説明されるケースが多いようですが、最初から面積図で教えると、その方法を単なる技法(テクニック)だとかんちがいする子どもが多いように思います。
「どちらか一方だけだったら」という考え方は算数・数学では大変重要な考え方です。まずはこの「一方だけと仮定する」考え方を教えてあげると、他の問題の理解も深まっていくと思います。　

「割合」と「速さ」は面積図で考えて

「割合」と「速さ」は、苦手になりやすい単元です。割合や速さの概念そのものが、個数、回数、人数などの量と比べ、具体的にイメージしにくいためかもしれません。

「割合」は、比べられる量がもとにする量に対してどのくらいの値になるかを示すもので
比べられる量÷もとにする量　
で求められます。

「速さ」は、1時間、1分、1秒といったもとになる時間あたりに移動する道のりを表し、
道のり÷時間
で求められます。

つまり、「速さ」は割合の一種で、考え方は同じといえるのです。
「割合」も「速さ」も　もとにする量×割合＝比べられる量　　速さ×時間＝道のり　というように、かけ算が基本形ですから、
どちらも、以下のような　たて×よこ＝面積　というかけ算の面積図で考えるとわかりやすいでしょう。

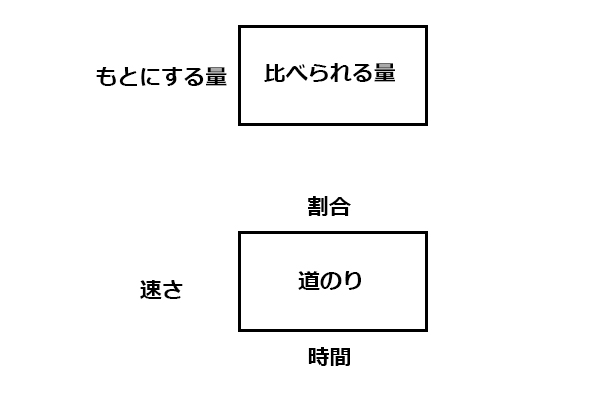
子どもたちは、「1000円の30％はいくら？」といった問題は、「1000×0.3＝300で300円」と、かけ算ですぐ答えを出せるのですが、
「□円の30％は300円」となると、どの数字をどの数字でわるのか、かけるのかわからなくなってしまうことがよくあります。その場合、この面積図を思い出せれば、迷いにくくなります。

「割合」は算数の中でも非常に重要な概念です。「割合」の基礎をマスターしていれば、今後さまざまな問題に応用が可能ですので、お子さまの理解が不十分だと感じたら、ぜひ基本に戻って復習しなおしてください。

（筆者：金廣志）