算数の図形問題が苦手。思い込みで解こうとする小4女子を持つ母親の悩み
図形問題を思い込みや当て推量で解こうとしてうまくいかない……。大ざっぱな性格の小4女子を持つ母親からの悩みに、平山入試研究所の小泉浩明氏が指導法をアドバイス。
＊＊＊
【質問】
まだ平面図形しか出ていませんが、かなり苦手です。図をきちんと見ないで、自分の思い込みで解いている気がします。たとえば「円の中に点があれば、半分のところになくても半分に割れる……」と考えてしまいます。（小4女子の母親）
【小泉氏からのアドバイス】
思い込みが激しいタイプに多いケースです。かつて、平面図形の問題に、「角Aは45度（くらい)だから、三角形ABCは直角二等辺三角形で……」と考える子どもがいました。「何で45度なの？」と尋ねると、「そのくらいに見える」という答え。これでは正解を得られません。角Aが45度というのなら、「これこれこうだから」という“根拠”が必要だと理解させましょう。
ただし、このような当て推量も無意味ではありません。算数や数学で大切な「ひらめき」に近い感覚でもあります。「そんな適当に考えていてはダメ！」と否定せず、「角Aが45度なら解けそうね。でも、45度である理由はある？ なければ45度とは決められないよ」と、推測に続けて「根拠」も考えるように促すとよいでしょう。
物事を考えるには、2通りの方法があります。一つは、現時点からさまざまな条件をつなぎ合わせて結果としてAという事象に到達する方法。もう一つは、Aという事象を最初に思い付き、それを実現するために現時点とAを結ぶ道をあとでつなぐ方法です。前者は積み上げ型、後者は発想型といえるでしょう。
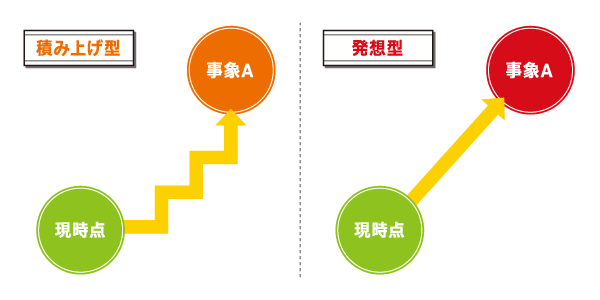
発想してもそれを現実の事象とするための努力がなければ、事象Aを事実として受け入れることはできません。上のような図を用いて、「あなたの考え方はよいけれども、この部分が足りない」と目で見える形で示すと納得が早いかもしれません。
