【微分法】微分係数g’(t)が表すもの
g’(t)とは直線を微分しているのですか?曲線だと接線を表すのは知ってますが、直線だと何をしているのか、わかりません。②は何をしているのですか?
進研ゼミからの回答
数学の勉強にがんばって取り組んでいますね。質問をいただいたのでお答えします。
【質問内容】
【問題】

【解答解説】から抜粋部分

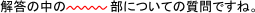
【質問への回答】
「g’(t)」というのは,
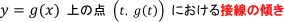
を表しています。
「直線」の場合は, 微分すると「定数」になり, これは「もとの直線の傾き」に一致します。
「曲線」の場合は, 微分すると「接線の傾きを表す関数」が出てきます。
(「接線」を表すわけではなく, 「接線の傾き」を表すことに注意しましょう。)
◆「f'(t)=g'(t)」……②」の意味
これは, y=f(x)と y=g(x)2つの関数において
「x=t における接線の傾きが同じになる」
ということを表しています。
ここでは, y=g(x)は直線になるので, 「f'(t)=g'(t)」というのは
「x=t における y=f(x) の接線の傾き」=「直線 y=g(x)の傾き」
という意味になります。
というわけで, 最終的な回答は, a>1となります。
以上のことを参考にして, もう一度考えてみてくださいね。
【学習アドバイス】
関数を微分して出てくるのは「接線の傾きを表す関数」になります。
直線(1次関数)の場合は, 微分すると その直線の傾き(定数)になるので,
ここでそのことをしっかり理解しておきましょう。
「2曲線y=f(x), y=g(x)が, x=tで接する」⇔「f(t)=g(t)かつ f'(t)=g'(t)」
これは, 一般に2曲線が x=tで共通の接線をもつための条件です。
重要な性質なので覚えて使いこなしていきましょう。
では, この調子でゼミ教材の問題にどんどん取り組み, 実践力を養っていってくださいね。
応援しています!
















