微分法|接線の本数と方程式の解の個数の関係|数学Ⅱ|定期テスト対策サイト

数学Ⅱ 定期テスト対策【微分法】接線の本数と方程式の解の個数の関係

【微分法】接線の本数と方程式の解の個数の関係

「接線が3本引けるのは、方程式②が異なる3つの実数解をもつとき」となっているのですが、それがなぜだかわかりません。

進研ゼミからの回答

こんにちは。
早速いただいた質問について回答します。

【質問内容】
【問題】
$問題文$

【解答解説】から抜粋部分

$【解答解説】から抜粋部分$

接線がちょうど3本引けるのは, 方程式②が異なる3つの実数解をもつとなっているのですが, それがなぜ
だかわかりません。
という質問ですね。

【質問への回答】
問題の曲線C上の接線の方程式を

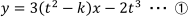
$y=3(t^2-k)x-2t^3…①$

としたので, ①が点(1,-2)を通るとすると, ①に, x=1, y=-2 を代入しても式が成り立つことになりま
す。
実際に代入すると,

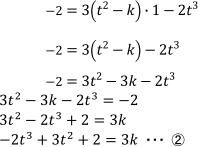
$-2=3(t^2-k)･1-2t^3　-2=3(t^2-k)-2t^3　-2=3t^2-3k-2t^3　3t^2-3k-2t^3=-2　3t^2-2t^3+2=3k　-2t^3+3t^2+2=3k…②$

と変形できて, ②はtについての方程式となります。
tは接点のx座標を表していますから, 方程式②の異なる実数解の個数と同じだけ接点がある, つまり, 異な
る実数解の個数が接点の個数と一致する, というわけです。

一方, 3次関数では, 接点の個数と接線の本数は一致するので, 接点が3個あれば, 接線も3本あります。
だから, 点(1,-2)を通る接線が3本引けるならば, 方程式②が異なる3つの実数解をもつ, ということになる
のです。

【学習アドバイス】
接線の本数を, 方程式の解の個数に置き換えて解く方法はよく使われます。
3次関数までは, 接線の方程式から,
問題の条件を満たす方程式をつくったとき,
(接線の本数)=(接点の個数)=(方程式の異なる実数解の数)
という関係になるので, 覚えておきましょう。

今後も『進研ゼミ高校講座』を使って, 得点を伸ばしていってくださいね。