【微分法】極大,極小を与えられたときの条件
「x=3で極小値をとるから,f′(3)=0 」と書かれていますが,このf′(3)=0は傾きが0だということを表しているのでしょうか。あまりイメージができません。回答よろしくお願いします。
進研ゼミからの回答
こんにちは。
いただいた質問について,さっそく回答いたします。
【質問の確認】

の解答で,
「x=3で極小値をとるから,f′(3)=0」と書かれていますが,このf′(3)=0は傾きが0ということを表しているのでしょうか? イメージができません。
というご質問ですね。
【解説】
≪ 極大・極小について ≫
一般に,f(x)の増加と減少が変わるところで,f(x)は「極大・極小」になるといい,関数f(x)の増減は微分係数f′(x)の符号で判断することができます。
グラフが単調に増加(接線の傾きが正)する区間の微分係数・・・ f′(x)>0
グラフが単調に減少(接線の傾きが負)する区間の微分係数・・・ f′(x)<0
グラフがx軸に平行(接線の傾きが0)である区間の微分係数・・・ f′(x)=0
つまり,極値となるのはf′(x)の符号が変化する境界であり,このとき,「f′(x)=0」であることが前提です。
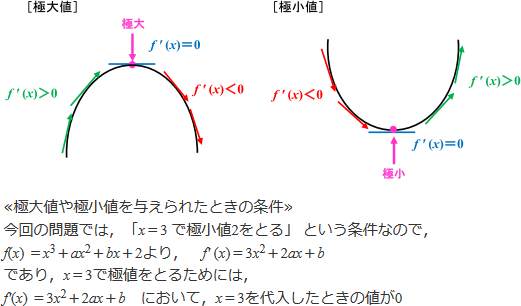
つまり,
f′(3)=0
という式が成り立たなくてはならないのです。
また,
「f′(3)=0」 は,y=f(x)のグラフで,x=3における接線の傾きが0である
ことを意味します。
そして,上の図のように,接線の傾きの変化に着目すると,
極値に近づくにつれて,傾きの絶対値は小さくなっていき,
極値では接線はx軸に平行,すなわち傾きは0になる
ことがわかります。
これで極値と接線の関係はイメージできましたか?
【アドバイス】
「 f′(x)<0 → f′(x)=0 → f′(x)>0 」 あるいは 「 f′(x)>0 → f′(x)=0 → f′(x)<0」 のようにf′(x)の符号の変化とf(x)の増加,減少の様子を結びつけてイメージできるようにしておきましょう。
増減表を作成してグラフをかく手順もしっかりマスターすることが大切です。
それでは,これで回答を終わります。
これからも,『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。
















