【2次関数】「2次関数のグラフとx軸の共有点」と「2次方程式の解」
「2次関数のグラフとx軸の共有点」を求めるのに,「2次方程式」を解くのはなぜ?
進研ゼミからの回答
こんにちは。
いただいた質問について,さっそく回答いたします。
【質問の確認】
「2次関数のグラフとx軸の共有点」を求めるのに,「2次方程式」を解くのはなぜ?
というご質問ですね。
【解説】
≪まずは復習から ~y軸との共有点~≫
次のような1次関数は,中学で学びましたね。まずは,これを例に,グラフと切片の関係をつかんでいきましょう。

このグラフ(直線)は,2点 (0,1),(1,3) を結んでかくことができます。
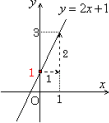
ここで,y切片,つまり,y軸との共有点の座標は1ですね。式で,y= ax+bのbが,y軸との共有点の座標だと覚えていればすぐにわかりますが,ここでは,y軸との共有点の座標が1になる理由を考えてみましょう。
y軸上の点は,
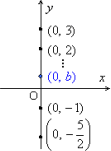
のように,すべて (0,b) の形で表すことができます。つまり,x座標は,0ですね。y切片を求めるには,x座標が0となるy=2x+1のグラフ上の点の座標,つまり,x=0のときのy座標を求めればよいのです。
y= 2x+1に,x=0を代入して,
y=2×0+1 =1
よって,y切片は1になるのです。
≪1次関数のグラフとx軸との共有点は・・・?≫
では,x軸との共有点はどのようにして求めればよいでしょうか。
(1)の結果から予測すると,y=2x+1に,y=0を代入すればよいのです。というのも,x軸上の点は,
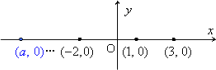
このように,すべて (a,0) の形で表すことができます。したがって,y座標が0となるグラフ上の点のx座標,つまり,y=0のときのx座標を求めればよいのです。
y=2x+1に,y=0を代入して,
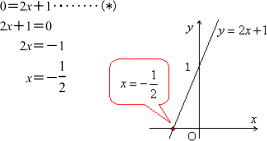
よって,この1次関数のグラフとx軸の共有点を求めるとき,(*)という式になりました。これは,1次方程式ですね。つまり, 1次関数y=ax+bのグラフとx軸の共有点のx座標は,1次方程式ax+b=0の解である,といえるのです。
それでは,これで回答を終わります。
これからも,『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。
















