【2次関数】文字定数の場合分けでの,<と≦の使い分け
文字を含む2次関数の最大値や最小値を求める問題で,場合分けの仕方を決めるとき,1≦a≦3,3<aとしたらよいか,1≦a<3,3≦a としたらいいのか,わかりません。どんな基準で場合分けをしたらいいですか。
進研ゼミからの回答
こんにちは。
いただいた質問について,さっそく回答いたします。
【質問の確認】
【問題】
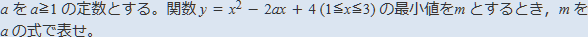
上の問題で,場合分けの仕方を決めるとき,1≦a≦3,3<aとしたらいいか,1≦a<3,3≦a としたらいいのか,わかりません。どんな基準で場合分けをしたらいいですか。
というご質問ですね。
【解説】
2次関数の最大値・最小値を求める問題では,「グラフ」と「定義域」の位置関係を調べることが定石です。
しかし,「グラフ」と「定義域」のどちらかに文字が入ったとき,最大値・最小値が1つの式では表せないことがあります。
そのようなときに,次の問題のように,場合分けをしますが,範囲に「ヌケモレ」がなければ,模範解答と≦,<が違っていても,正解と考えてOKです。
【問題】
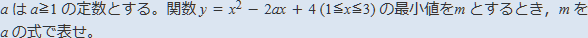
まず,この問題の解答を確認しましょう。
【解答】
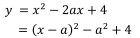
したがって,このグラフは,下に凸の放物線で,軸の方程式はx=aである。
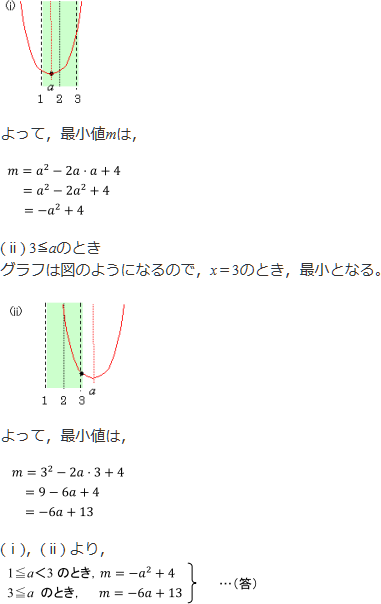
(ⅰ) 1≦a<3のとき
グラフは図のようになるので,x=aのとき,最小となる。
≪場合分けのポイント≫
気をつけるポイントは,
範囲に「ヌケモレ」がないか
の1点です。これらをクリアできるように,<と≦を使い分けて場合分けの範囲を決めればよいのです。
基本的には,この条件を満たしていれば,<と≦は,自分の都合のいいように決めることができます。
上の解答の場合分けを見ると,1≦a<3,3≦aとなり,ヌケモレはありませんね。
では,この場合分けのa<3,3≦a の部分を,a≦3,3<a としてもよいかどうか,見ていきましょう。
まず,(ⅰ) と (ⅱ) の境目であるa=3に注目してみましょう。
(ⅰ),(ⅱ) の最小値に,a=3を代入してみると,
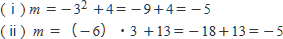
となり,どちらも同じ値になります。つまり,a=3は (ⅰ),(ⅱ) のどちらの場合分けの範囲に入れてもよいので,
(ⅰ) 1≦a≦3 のとき
(ⅱ) 3<aのとき
と場合分けしてもよいことがわかります。すなわち,
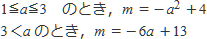
としても正解,と言えるのです。
【アドバイス】
場合分けは,「ヌケモレ」がなければ,模範解答と≦,<が違っていても,正解と考えて大丈夫です。
問題を解いたあと,きちんと範囲にヌケモレがないか,見直しをするようにしましょう。
それでは,これで回答を終わります。
これからも,『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。
















