【2次関数】場合分けを考える時のグラフについて
こんにちは。いつもお世話になっています。
二次関数の場合分けを考える時のグラフについて質問があります。
教えてください。
解説ではグラフを書いて考える事になっています。
このグラフなのですが、自分で、書くことは出来るのですが、書いたグラフが、どれを指すのか分かりませ
ん。
とくに文字を含む場合は、もうお手上げです。
(tは0より大きいのかなぁ?なんて迷ってます)
グラフがどれを指しているのか分かるようになりたいです!
教えてください!
進研ゼミからの回答
こんにちは。がんばって勉強していますね。
では、早速質問にお答えします。
【質問の確認】
【問題】

において
最大値・最小値を求めるときの場合分けのグラフについてですね。
【解説】
グラフをかくときのポイントは、軸と定義域の位置関係をしっかりとつかむことが大切です。 上の問題では、
(1)a<1 (2)a=1 (3)1<a という3つに場合分けします。
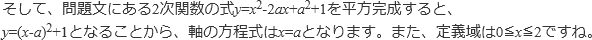
つまり、問題文の場合分けのポイントになっている「1」という数字ですが、
これは定義域0≦x≦2の中央の値になっています。
このことから、問題文の場合分けを言葉で表現すると、
(1)a<1 →軸が定義域の中央よりも左にある
(2)a=1 →軸が定義域の中央
(3)1<a →軸が定義域の中央よりも右にある
ことになります。よって、このようなグラフをかくと、
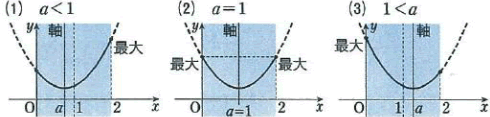
となるのです。これより、最大となるxの値は、
(1)定義域の右端のx=2のとき
(2)定義域の両端の、x=0,x=2のとき
(3)定義域の左端のx=0のとき
となることがわかるのです。
今回の回答を参考にして、まずは、軸と定義域の位置関係を考え、グラフがどのようになるかを考えてみてください。
【アドバイス】
このような場合分けをするときのポイントは、軸と定義域の位置関係になります。
2次関数のグラフの形(上に凸か下に凸か)や、最大値を求めるときと最小値を求めるときで、場合分けの仕方が異なります。
それぞれの場合で、どのように場合分けすればよいかを、問題演習を繰り返すことで、正しく理解しておきましょう。
では、今後も『進研ゼミ高校講座』を活用して、得点アップをめざしましょう!
















