【式と証明】複雑な式の因数分解
x^3+xy-y-1のような複雑な式の因数分解はどうやればいいですか?
進研ゼミからの回答
こんにちは。
いただいた質問について,さっそく回答いたします。
【質問の確認】

【解説】
複雑な式でも,文字が1種類のときの因数分解と同じ手順で,
①共通因数をくくり出す。
②公式を使う。
が基本です。
しかし,これだけでは因数分解するときの糸口が見えないときもあります。
そんなときには,以下の方法も用いて因数分解していきましょう。

①②のときは,①→②の順番で行いますが,③④には決まった順番はありません。2種類以上の文字の式の場合は,①~④の順番は考えず,式の特徴から判断し,使えそうな手順を選んでいきましょう。
では,上の手順を利用して,実際に,x3+xy-y-1を因数分解してみましょう。

今回の因数分解では,④の方法は利用していませんが,例えば,(a+b)(a+b-2)-15を因数分解するときには④を利用することが有効です。
実際に(a+b)(a+b-2)-15を因数分解してみましょう。「同じ文字の並び」であるa+bを1つのカタマリとみて,a+b=Xで置き換えます。すると,Xの2次式にでき,次のように計算できます。
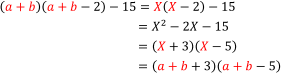
【アドバイス】
因数分解は今後いろいろなところで使うので,ここでしっかり習得してください。式の特徴から判断し,①~④の手順の中から使えそうな手順を選んでいきましょう。数多くの問題を解くことにより,よりよい手順を速く選べるようになるので,頑張ってください。
それでは,これで回答を終わります。
これからも,『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。
















