【数と式】絶対値と場合分け
0≦x≦2のとき
│xー2│は
もし、xが2ならば、0になります。
そのときも含めて
なぜー(xー2)をするのですか?
あと、
場合わけの
コツをおしえてください!!
進研ゼミからの回答
こんにちは。
いただいた質問について、早速、回答します。
【質問の確認】
【問題】
方程式|x|+|x-2|=4を解け。
について、
【解答解説】

の場合分け(ⅱ)のとき、なぜx=2のときも含めて|x-2|を-(x-2)とするのか、ということと、場合分けのコツについてですね。
【解説】
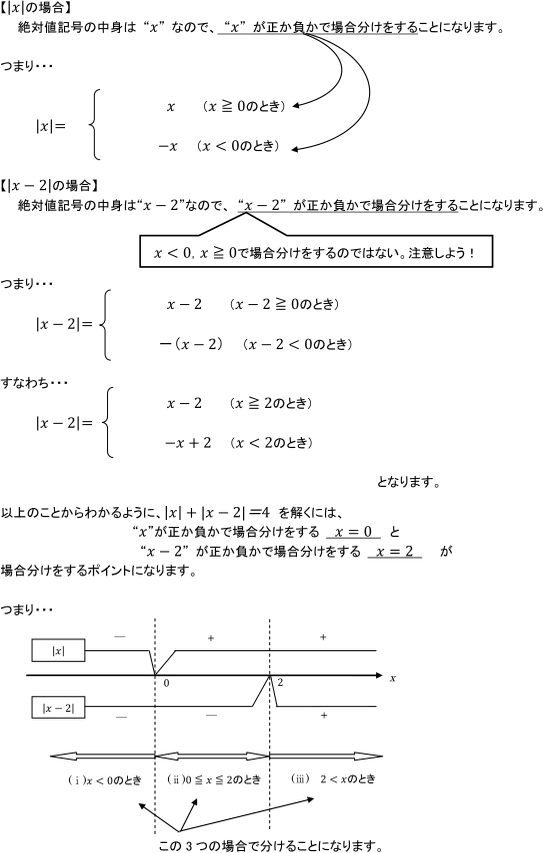
まず、問題を通して場合分けのしかたを先にみていきましょう。
問題に含まれている|x|と|x-2|について考えてみます。
【アドバイス】
絶対値記号のはずし方についてどのように考えればよいのか納得してもらえたでしょうか。
絶対値記号の中身がどんなに複雑になってもはずしかたの基本は変わりません。
記号の中身が正か負かに注意して考えていきましょう。
今回は
(ⅰ)x<0のとき、 (ⅱ)0≦x≦2のとき、 (ⅲ)2<xのとき
で場合分けしましたが、等号はどこに含めても構いません。
(ⅰ)x≦0のとき、 (ⅱ)0<x≦2のとき、 (ⅲ)2<xのとき
などでもOKです。
ここで、(ⅱ)と(ⅲ)の境界x=2についてみると、
『x-2』にx=2を代入しても、
『-(x-2)』にx=2を代入しても
0になりますね。
したがって、x=2については(ⅱ)と(ⅲ)のどちらの場合に含めてもいいのです。
よく復習してこの機会に絶対値記号を含む方程式をしっかりマスターしておきましょう。
これからもがんばってくださいね。