【数と式】因数分解をするときの途中式について
教材の解説を読んでいたところ、なんでこの式からこの式になるんだというところを見つけたので質問させていただきます。
x^2+xy-2x+3y-15=(x+3)y+x^2-2x-15
=(x+3)y+(x+3)(x-5)・・・①
=(x+3)(x+y-5)・・・②
なぜ①の(x+3)yのyが②の(x-5)に入るのかが分かりません。
解説お願いします。
進研ゼミからの回答
こんにちは。
早速いただいた質問について、お答えしていきましょう。
【質問の確認】
【問題】
次の式を因数分解せよ。
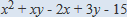
について
【解答解説】
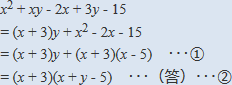
の①から②への変形についてですね。
【解説】
ここでは、因数分解を考えているので、
『①では (x+3) が共通因数』になっている
ことがポイントです。
『共通因数があればそれをくくり出す』
という考え方を学習しています。ここでも、それを使っていますよ。

上に示したような考え方なので、
これは「分配法則」の逆の計算です。
a(x + y) を分配法則で展開すると、ax + ay になりますね。
これにしたがって、
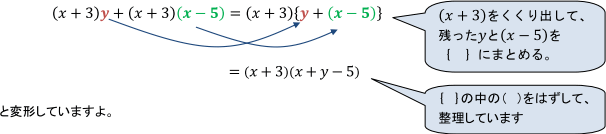
【アドバイス】
『共通因数をくくり出す』考え方は、因数分解でよく利用する考え方です。因数分解を考えるときには、最初に共通因数があるかどうかを考えて、あるときにはくくり出してから公式をあてはめるようにしましょう。
これからも『進研ゼミ高校講座』を使って、数学の力を伸ばしていってくださいね。
















