【数と式】対称式はどんなとき使うんですか?
(2)で(x+y)^2=x^2+2xy+y^2 の1行目の式変形をしているのはどうしてですか?
対称式の説明も読んだのですが、よくわかりません。
進研ゼミからの回答
こんにちは。がんばって勉強に取り組んでいますね。
いただいた質問について、さっそく回答させていただきます。
【質問の確認】
【問題】
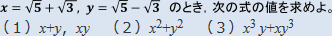
について、
【解答解説】から抜粋部分
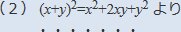
上記のように、1行目の式変形をしているのはどうしてなのか、
対称式の説明を読んでも、よくわからなかった、とのご質問ですね。
さっそく確認していきましょう。
【解説】
「1行目の式変形をしているのはどうしてなのか」ということですが「その方が簡単に計算ができるから」です。
値を求める問題では、計算に手をつける前に、まず「式の特徴」をつかみましょう。
それによって、効率のよい方針が見つかることがあります。
この問題で値を求めたい式は、対称式と呼ばれる特徴のある式なのです。
「x,y を入れ換えても、もとの式と同じになる式」をx,y についての対称式という。
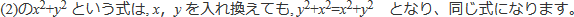
つまり対称式といえますね。
対称式には次のような性質があります。
x,y についての対称式は基本対称式 x+y,xy で表すことができる。
そこでx,y についての対称式の値を求めるような問題では、次の手順が定石となります。
(ⅰ)まず、基本対称式 x+y,xy の値を計算する。
(ⅱ)与えられた対称式を基本対称式で表す。
(ⅲ)(ⅱ)の式に(ⅰ)の結果を代入する。
では、(2)を上の定石にあてはめてやってみましょう。

⇒(1)でx+y,xy の値を求めるようになっていたのも、あとの問題を計算するための誘導だったわけです。
このあたりも実は方針立てのヒントになっているので、問題を解くときは、問題文自体にもアンテナを張っておくといいですよ。
同様に(3)の問題にも挑戦してみましょう。
x,yに直接値を代入するより、はるかに楽に計算できますよ。
x,yが複雑な値であるほど、計算する式が複雑であるほど、この方針での計算が有効になります。
ぜひこの機会に対称式の性質をマスターしておきましょう。
【アドバイス】
計算問題において、問題を解く方針を立てるとき、まず「式の特徴」をつかむことは、
効率よく解くためにとても有効です。式の特徴にあったワザを身につけておくと
これから色々なシーンできっと役に立つので、1つひとつマスターしていきましょう。
効率のよい解法は、時間の短縮だけでなく、計算ミスの防止にもつながりますよ。
















