【図形と計量】180°-θの三角比
解説にcosC=cos(180°-A)=-cosA
と書かれているんですが,
どうしてcos(180°-A)が-cosA
になるのかがわかりません。
進研ゼミからの回答
こんにちは。
いただいた質問について,さっそく回答させて頂きます。
【質問の確認】
どうしてcos(180°-A)=-cos A
になるのかがわかりません。
というご質問ですね。
【解説】
cos(180°-A)=-cos A であることは,次の「180°-θ の三角比」の関係式からわかります。
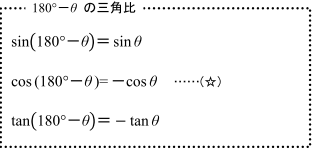
上の(☆)の式において,θ をAで置き換えるとcos(180°-A)=-cos Aが得られますね。上の3つの関係式が成り立つことは,単位円の図をかいて確認しましょう。下の図のように,角θに対する動径OPと角180°-θ に対する動径OQを単位円上にとると, 点Qのy座標は点Pの y座標に等しく,点Qのx座標は点Pのx座標と符号が反対になることがわかります。
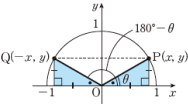
よって,三角比の定義より,
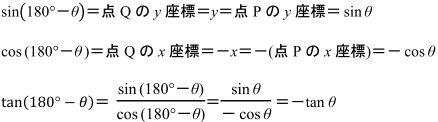
が成り立つことがわかりますね。
【アドバイス】
180°-θとθの三角比の関係は,公式として暗記するのではなく,上のような図をかいて求められるようにしておくのがよいですね。
では,これからも『進研ゼミ 高校講座』を活用して,得点を伸ばしていってくださいね。
















