(受験生にオススメ)【式と証明】2数の和・差と偶奇性の関係
どうしてx+yとx-yの差を求めることでx+yとx-yの偶数奇数が一致することが証明できるのでしょうか?
進研ゼミからの回答
こんにちは。
では, いただいた質問について, 回答します。
【質問内容】
【問題】
次の問いに答えよ。
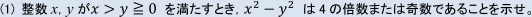
【解答解説】から抜粋部分

x+yとx-yの差を求めたとき, (★)部で, x+yとx-yの偶奇が一致する理由ですね。
【質問への回答】
わかりやすいように, ふたつの値を, AとBとして簡単に証明しておきます。

この問題では, Aがx+y, Bがx-yとあてはめて, とらえましょう。
【学習アドバイス】
今回のように, なぜ?と, 思ったときは, 自分自身で, 証明を考えてみましょう。
整数の偶奇が関係しているので, 文字m, nなどを用いて, 条件を表してみるのがオススメです。
イメージだけでなく, 式として示してみると, とてもわかりやすくなりますよ。
ゼミの教材を学習に役立てて, 力をつけていってください。応援しています。
















