式と証明|相加平均と相乗平均の等号成立条件|数学Ⅱ|定期テスト対策サイト

数学Ⅱ 定期テスト対策【式と証明】相加平均と相乗平均の等号成立条件

【式と証明】相加平均と相乗平均の等号成立条件

どうして等号成立条件がa-b=0なんでしょうか？
問題ではa+bしか出てこないですよね？

進研ゼミからの回答

こんにちは。
いただいた質問について、早速、回答します。

【質問の確認】

【問題】
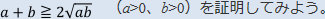
$a＋b≧2√ab（a＞0、b＞0）を証明してみよう。$
で　問題ではa+b しか出てこないのに、

【解答解説】の証明
$等号が成り立つのは、a-b=0、すなわちa=bのとき。･･･（＊）$
の（＊）で等号成立条件が「a-b=0」となることについてですね。

【解説】

相加平均・相乗平均の大小関係を証明するところでの、等号成立条件について・・・
どうして、a-b=0なのか？という質問ですね。

不等式の証明の基本は、「差をとって、符号を調べる」

ことは、よく理解できていますね。
$これを踏まえて、相加平均・相乗平均の大小関係を証明するとき、根号を含むことから、2乗して差をとり、（左辺）－（右辺）≧0を導いたときの式が、ポイントです。この式で等号成立条件を考えます。等号が成り立つのは、（）の中身が0のとき。つまり、a-b＝0のときとなります。$
不等式を証明する時には、等号がつくのか、つかないのか、意識することは大切です。
この点に注意しているのが良いですね。