【式と証明】「実数の2乗は0以上」の使い方
式の証明で「実数の2乗は0以上」がうまく使えません。
a,bは実数として,a^2-ab+b^2≧0の証明で,(実数)^2≧0だから,a^2≧0,b^2≧0ですよね?
-abはどうなるのですか?
進研ゼミからの回答
こんにちは。
いただいた質問について,さっそく回答いたします。
【質問の確認】
式の証明で「実数の2乗は0以上」がうまく使えません。
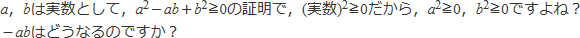
というご質問ですね。
【解説】

平方完成の手順


最後に,以上のことをまとめておきます。
2次式が0以上になることを証明する場合は,
平方完成を用いて,式全体で,(実数)2や (実数)2+(実数)2などの形をつくることを考える。
【アドバイス】
2次式が0以上であることを証明するときの式変形は,因数分解の公式を使ってうまくいくこともありますが,基本になるのは平方完成です。いろいろな式で練習し,平方完成を利用して,(実数)2の形がつくれるようにしておきましょう。
それでは,これで回答を終わります。
これからも,『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。
















