【式と証明】相加平均,相乗平均
相加平均,相乗平均ってそもそも何ですか? 「平均」なんですか? どうして証明に使っているのですか? 式の説明をしてほしいです。
進研ゼミからの回答
こんにちは。
いただいた質問について,さっそく回答いたします。
【質問の確認】
相加平均,相乗平均ってそもそも何ですか? 「平均」なんですか? どうして証明に使っているのですか? 式の説明をしてほしいです。
というご質問ですね。
【解説】
≪そもそも相加平均,相乗平均とは?≫
【相加平均】

【相乗平均】
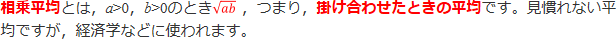
a>0,b>0という条件がつくのは,ルートの中は正になるという約束があるためです。
≪相加平均と相乗平均の大小関係≫
この2種類の「平均」の大きさを比べると,常に,(相加平均)≧(相乗平均)となります。
これが,「相加平均と相乗平均の大小関係」です。
a≠b のとき,(相加平均)>(相乗平均)・・・・・・①
a=bのとき,(相加平均)=(相乗平均)・・・・・・②
①と②を合わせて,(相加平均)≧(相乗平均)となります。
さて,この①と②の関係が本当に成り立つかどうかを見てみましょう。
【a ≠ b のとき,(相加平均)>(相乗平均)・・・・・・①の例】
例えば,a = 3,b = 12 のとき,

したがって,7.5 > 6 となるので,①の(相加平均)>(相乗平均)が成り立ちます。
【a = b のとき,(相加平均)=(相乗平均)・・・・・・②の例】
a = 4,b = 4 のとき,
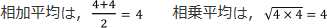
したがって,4 = 4 となるので,②の(相加平均)=(相乗平均)が成り立ちます。
このように,常に,(相加平均)≧(相乗平均)となるのです。
◎まとめ
◆a,bが正の数であれば,常に,(相加平均)≧(相乗平均)の関係が成り立ちます。
つまり,

したがって,=が成り立つのは,a = b のときだとわかりますね。
この「相加平均,相乗平均の大小関係」は,a > 0,b > 0 のときに,「常に」成り立つので,不等式の証明では,「証明の道具」として使うことができるのです。
◆相加平均と相乗平均の大小関係は,a,b がともに正の数(a > 0,b > 0)でなければ成り立つとは言えません。そこで,これを使うときは,必ず,a,b がa > 0,b > 0であることを確認して使うようにしましょう。
【アドバイス】
「相加平均と相乗平均の大小関係」を使うと楽に証明できる場合もあるので,便利な「証明の道具」として使えるようにしておくとよいでしょう。ただし,「相加平均と相乗平均の大小関係」が使えるのは,a,b が a>0,b>0がである場合だけであることに注意しましょう。
それでは,これで回答を終わります。
これからも,『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。
















