図形と方程式|接線の公式の使い方について|数学Ⅱ|定期テスト対策サイト

数学Ⅱ 定期テスト対策【図形と方程式】接線の公式の使い方について

【図形と方程式】接線の公式の使い方について

円と直線の位置関係からでなく、接点の座標を設定して答えを求めるやりかたがわからない

進研ゼミからの回答

こんにちは。
いただいた質問について、早速、回答します。

【質問の確認】

【問題】
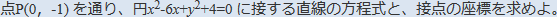
$点P(0, -1)を通り、円x二乗-6x+y二乗+4=0に接する直線の方程式と、接点の座標を求めよ。$

について、

【解答解説】
円と直線の位置関係からでなく、接点の座標を設定して答えを求める

解き方について、のご質問ですね。

【解説】

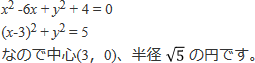
$x二乗-6x+y二乗+4=0　(x-3)二乗+y二乗=5　なので中心(3,0)、半径ルート5の円です。$

接線の公式を使うためには中心が原点でなければいけません。そこで円の中心が(0，0)になるように、平行移動した状態で接線を求め、それを逆に平行移動して元に戻すという手順で考えます。

$x軸方向に-3平行移動すると円はx二乗+y二乗=5になります。また問題では「(0,-1)を通る」という条件でしたが、この(0,-1)も同様にx軸方向に-3平行移動すると、(-3, -1)になります。そこで(-3, -1)を通り、x二乗+y二乗=5に接する接線を考えます。$

【円の接線の方程式】
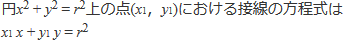
$円x二乗+y二乗=r二乗上に点(x1, y1)における接線の方程式はx1x+y1y=r二乗$

$接点の座標をP(x1, y1)とおくと、接線の方程式はx1x+y1y=5 … まる1$

これが(‐3，‐1)を通るので

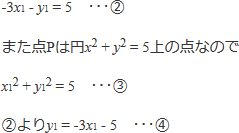
$-3x1-y1=5 … まる2　また点Pは円x二乗+y二乗=5上の点なのでx1二乗+y1二乗=5 … まる3　まる2よりy1=-3x1-5 … まる4$

④を③に代入すると

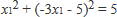
$x1二乗+(-3x1-5)二乗=5$

展開して整理すると

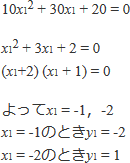
$10x1二乗+30x1+20=0　x1二乗+3x1+2=0　(x1+2)(x1+1)=0　よってx1=-1, -2　x1=-1のときy1=-2　x1=-2のときy1=1$

これらを①に代入すると接線の方程式は

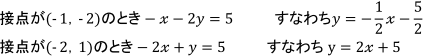
$接点が(-1, -2)のとき-x-2y=5 すなわちy=-1/2x-5/2　接点が(-2, 1)のとき-2x+y=5 すなわちy=2x+5$

ただしこれは平行移動した後の接線なので、元に戻さなければいけません。
接点と接線をともにx軸方向に3平行移動します。

y=f(x)のグラフをx軸方向にpだけ平行移動したグラフを表す式はy=f(x-p)

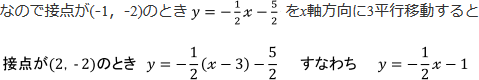
$なので接点が(-1, -2)のときy=-1/2x-5/2をx軸方向に3平行移動すると接点が(2, -2)のときy=-1/2(x-3)-5/2すなわちy=-1/2x-1$

接点が(‐2，1)のとき y = 2x + 5 をx軸方向に3平行移動すると

接点が(1，1)のとき y = 2(x - 3) + 5 すなわち y = 2x - 1

となります。