【数と式】無理数の整数部分,小数部分の求め方
「√11の整数部分,小数部分を求めなさい。」
という問題で,どうして,3≦√11<4という式が出てくるのか,わかりません。
そして,この整数部分が3だと,どうしてわかるのですか?
進研ゼミからの回答
こんにちは。
いただいた質問について,さっそく回答いたします。
【質問の確認】

【解説】
≪整数部分,小数部分の意味≫
例えば,2.236という数では,整数部分は2,小数部分は0.236 となります。
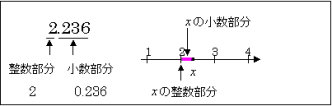
さて,簡単な数の場合,上のように見ればわかりましたが,これを手順として表すと次のようになります。
ある数■の整数部分,小数部分を見つける問題の解き方の手順
①n≦■<n+1 となる整数 nを見つける。(整数 nが整数部分となります。)
②「(整数部分)+(小数部分)=(もとの数)」を使って,小数部分を求める。
まず,手順を理解するために,先ほどの2.236を例に,大きな流れをつかみましょう。
【例1】
2.236の整数部分と小数部分を求めなさい。
手順① 2.236の整数部分を求める。
まず,2.236は,どんな整数の間にある数か,調べます。これを,数直線上に表してみると,
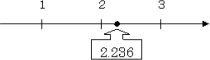
となり,2と3の間にあることがわかりますね。上で示した手順の①の書き方で表すと,2≦2.236<3となります。
したがって, 2.236の整数部分は2となります。
手順② 小数部分を求める。
「(整数部分)+(小数部分)=(もとの数)」ですね。この式を変形して,
「(もとの数)-(整数部分)=(小数部分)」とすれば,「小数部分」を求めることができますね。
つまり,2.236-2=0.236となり,小数部分は0.236となります。
これで,手順の概要はつかめましたか?
さて,無理数についても,基本的な考え方は同じです。
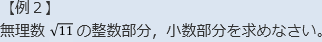
![[手順1]まずn≦√11<n+1となる整数nを求める。[手順2]小数部分を求める。◎オマケ◎](/teikitest/_resource/img/kou/math/k_m_114_5.png)
【アドバイス】
ある数■の整数部分を調べるときは,■が「連続した整数に挟まれる形」,すなわち,n≦■<n+1の形にすることがポイントです。
また,n≦■<n+1の形にできたあと整数部分を求めるときに,『n≦■<n+1 のとき■の整数部分はn 』ということを丸暗記するのではなく,数直線をかいたり,具体的な数で考えたりして,導けるようにしておくことで,ケアレスミスを防げるでしょう。
それでは,これで回答を終わります。
これからも,『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。
















