【三角関数】三角関数の合成について
sinθ+cosθをrsin(θ+α)の形に変形するときに,θ+4分のπとなるところはどのように出せばよいのでしょうか?教えてください!!
進研ゼミからの回答
いただいた質問にお答えします。
【質問の確認】
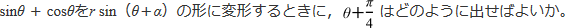
というご質問ですね。
【解説】
これは45°,45°,90°の直角三角形の辺の比からわかります。
sinθ+cosθをr sin(θ + α)と変形するときのα(-π<α≦π)を求める手順は次の通りです。
<sinθ+cosθをr sin(θ+α)と変形するときのα(-π<α≦π)を求める手順>
①sinθとcosθの係数に着目 → ここでは1と1
②P(1,1)を座標平面上にとる(右下の図)
③OPとx軸の正の向きとのなす角を見つける → これがα

となります。


となります。これは公式を忘れたときや三角関数の合成の問題を穴うめにしたときに使えますので,あわせて理解しておきましょう。
【アドバイス】
30°,60°,90°の直角三角形と45°,45°,90°の直角三角形の辺の比は覚えておいてください。
また,三角関数の合成は方程式や不等式の問題にも使います。
回答でも触れましたが,この公式は加法定理から導いたものです。加法定理は基本になる重要な定理なのでしっかり理解し,覚えてください。
それでは,これで回答を終わります。これからも『進研ゼミ高校講座』で確実に力をつけていってくださいね。
















