【図形と方程式】等距離にあるx軸上の点の座標の求め方
2点A、Bから等距離なのでAP=BPということはわかるがAP^2=BP^2 にする意味がよくわからない。
√にしてといたらだめなの?
進研ゼミからの回答
数学の勉強にがんばって取り組んでいますね。質問をいただいたのでお答えします。
【質問の確認】
【問題】
2点A(-2,1)、B(6,3)から等距離にあるx軸上の点Pの座標を求めよ。
について、
【解答解説】
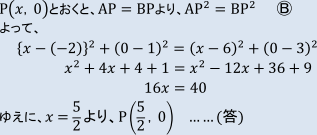
【解説】

【アドバイス】

では、この調子でがんばってゼミの教材の問題に取り組み、実戦力を養っていってくださいね
















