数学Ⅱ 定期テスト対策【複素数と方程式】整式の割り算の余りの求め方

進研ゼミからの回答

こんにちは。
いただいた質問について，さっそく回答いたします。

【質問の確認】

[問題 1]



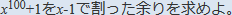
[問題 2]
P(x)をx-2で割った余りが５，x-3で割った余りが７のとき，P(x)を(x-2)(x-3)で割った余りを求めよ。

上の問題のように，次数の高い式の割り算や，割られる式がわからなくて割り算ができない場合に，どうやって余りを求めるのですか？
というご質問ですね。

【解説】

余りに関する問題でカギになるのは，「割り算について成り立つ等式」です。まずは，そこからスタートしましょう。

≪1. 自然数の「割り算について成り立つ等式」≫
まず，自然数の割り算を思い出してみましょう。例えば，19÷7は，




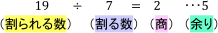
となり，これは，




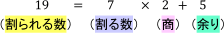
という等式に書き換えられましたね。これが自然数の「割り算について成り立つ等式」です。
注意したいのは，「余り」は「割る数」より小さくなるということです。もし，余りが割る数より大きければ，まだ割り算ができますね。だから，最後まできちんと割れば，必ず余りが割る数よりも小さくなります。

≪2. 整式の「割り算について成り立つ等式」≫
整式でも自然数の割り算と要領は同じです。



という式が得られ，これを書き換えると，




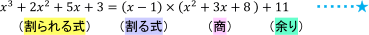
という等式になります。これが，整式の「割り算について成り立つ等式」です。
ここで，余り１１は定数であり，その次数は０だから，余りの次数は割る式x-1の次数１より低くなります。そうでなければ，もっと割ることができるはずですね。

≪3.余りの次数について≫　
上の説明のように，割り算では，余りの次数が割る式の次数より低くなることがポイントです。
割られる式P(x)の次数がどんなに大きくても，何次式かわからなくても，割る式が１次式なら余りは定数，割る式が２次式なら余りは １次式か定数，・・・ということがわかるのです。
したがって，a，b，cを実数とすると，

　P(x)を１次式で割った余りなら，定数a

　P(x)を２次式で割った余りなら，１次以下の式なのでax+b，


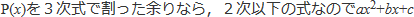
のように書き表すことができます。
これが，P(x)がわからなくても余りが求められる秘訣です。

≪4. 剰余の定理≫



つまり，P(x)をx-1で割った余りはP(1)，すなわち，割る式が０になる値を代入すれば余りが現れることがわかります。




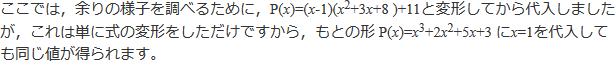
これが剰余の定理です。

剰余の定理

整式P(x)を１次式x-αで割った余りはP(α)

≪5. 余りの求め方≫
それでは，最初の問題を解いて，具体的に余りの求め方を考えてみましょう。




[問題2]の解答
この問題の場合，P(x)はわかりませんが，≪3.余りの次数について≫で考えた通り，
２次式(x-2)(x-3)で割った余りは１次以下の式ax+b(a，bは実数)と書くことができます。そこで，これを利用すると，解答は次のようになります。

P(x)を(x - 2)(x - 3)で割った商をQ(x)，余りを ax + b とすると，




x - 2 で割った余りが５だから，剰余の定理より，割る式 x - 2 が０になる値 x = 2 を(*)に代入して，




同様に，x - 3 で割った余りが７だから，x = 3 を(*)に代入して，




①と②を連立させて解くと，a = 2，b = 1
よって，P(x)を(x - 2)(x - 3)で割った余りは　2x + 1　･･････(答)

◎ まとめ
整式を割った余りを求める問題は次のことがポイントとなります。

■整式を１次式x-αで割った余りはx-αが０になる値x=αを代入して求める(剰余の定理)。

■整式を２次以上の式で割った余りは，(余りの次数)＜(割る式の次数)となるように余りをおいて，割り算について成り立つ等式をつくって求める。

【アドバイス】

割り算について成り立つ等式は，整式の割り算の基本となるので，しっかり身につけておいてください。
また，整式の割り算の余りを求める問題では，剰余の定理をうまく利用することもポイントになるので，いろいろな問題で練習しておきましょう。

それでは，これで回答を終わります。
これからも，『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。