(受験生にオススメ)【複素数と方程式】基本対称式を利用して高次方程式の実数解を求める方法について
x,yが実数でx+y=u,xy=vのとき,「u,vはu2-4v≧0を満たす」を求めるところで,なぜtについての2次方程式が出てくるのかわかりません。
進研ゼミからの回答
こんにちは。数学の勉強にがんばって取り組んでいますね。
質問をいただいたのでお答えします。
【質問内容】
【問題】
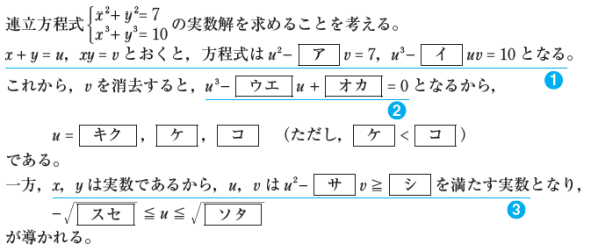
【解答解説】から抜粋部分

の,(★)部の式となる理由ですね。
【質問への回答】
「t」という文字が唐突に出てきているので, 何をやっているのか意味がよくわからず, とまどってしまったよう
ですね。この部分は次のように考えています。
一般に
xの2次方程式 (x-a)(x-b)=0 の解は, x=a,b
となるので, このことを逆に考えると
a,b を解とするxの2次方程式は (x-a)(x-b)=0 と表せる。
と言うことができます。
そして
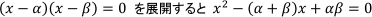
となるので, ここからわかることをまとめると
a,b を解とする▲の2次方程式は
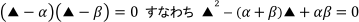
と表すことができる。

方程式の未知数▲の文字は通常は「x」を使いますが, ここでは問題文で既に使っているので, ▲のところ
にxを使うことができません。
ですから, まだ使っていない文字の中から とりあえず「t」を選んで
「x,yを解にもつtの2次方程式」は
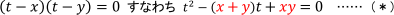
と表すことができる。
と考えているので, そのことをよく理解しておいてくださいね。
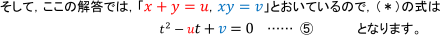
ここで, x, yについては, 問題文の最初に「実数解」となっているので,
⑤は実数解をもたなくてはいけませんから, ⑤が実数解をもつ条件を考えると,
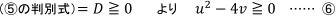
となります。
つまり, 解答では, (u-1)(u-4)(u+5)=0
u=-5, 1, 4 より,
3つの u の値を得ますが, ⑥は実は u と v の値には制限が加わることを示しているのです。
あとは「③と⑥から u, v の値を絞り込み, それらを⑤に代入して解く」ということをすれば, x, yの値が求め
られます。
【学習アドバイス】
一般に, 「a, bを解にもつ△の2次方程式」は
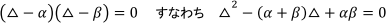
と表せるので, このことから
『a + b, ab の値がわかれば, a, b を解とする2次方程式を
つくることができ, その方程式を解けば a, b の値が求められる。』
と言うことができます。
この性質は「対称式の形で表された方程式」を解くときに特に役に立つものなので
『基本対称式(2数の和と積)がわかれば, その2数を解にもつ2次方程式がつくれる』
ということを覚えておいて, うまく利用していってくださいね。
では, この調子でゼミ教材の問題にどんどん取り組み, 実戦力を養っていきましょう。
応援しています!
















