【複素数と方程式】因数定理を利用するときのP(α)=0となるαの見つけ方
x^3-3x^2+6x-4=0を解くとき,(左辺)をP(x)とおくと,P(1)=0とありますが,
このxの値1はどうやって求めるのですか?
がむしゃらにやっても大変です。
進研ゼミからの回答
こんにちは。
いただいたご質問について, 早速回答させていただきます。
【質問内容】
【問題】
次の方程式を解け。
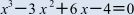
【解答解説】から抜粋部分

上のような問題で因数定理を利用して因数分解するときに, P(a)=0となる a をどうやって見つければよ
いですか, というご質問ですね。
【質問への回答】
因数定理を用いるにあたり, P(a)=0となるaを見つけるには, 以下の方法を利用しましょう。

━‥━‥━‥━‥━‥━‥━‥━‥━‥━‥━‥━‥━‥━‥━‥━‥━‥━‥━‥━‥━‥━‥
◎おまけ◎
ちなみに, このaの候補の中に P(a)=0 を満たすものがなければ, P(x)=0を満たす有理数は存在せず,
P(x)は有理数の範囲で因数分解できないことになります。
【学習アドバイス】
ここで紹介した方法をぜひ試してみてくださいね。
また, これが成り立つ理由はゼミの教材にも解説してありますので, 確認しておくとよいですよ。
これからも『進研ゼミ 高校講座』の教材を利用して, 力をつけていきましょう。
















