【2次関数】変域を調べる理由
新しい変数が現れたときに、変数をチェックする理由がわかりません。
あと、
x^2-2x=tから
t=(x-1)^2-1が成り立つのはわかりますが、
そこから、
t>=-1になる理由も分かりません。
よろしくお願いします。
進研ゼミからの回答
こんにちは。
いただいた質問について、さっそく回答させていただきます。
【質問内容】
【問題】

という問題の
【解答解説】から抜粋部分

の(★)の部分でtの変域をチェックする理由ですね。
【質問への回答】
本問のように関数の最小値や最大値を求めるときには, 「その関数の定義域を確認する」必要があります。
本問では定義域(xの条件)が特に与えられていないので, 「xはすべての実数を取り得る」という条件下で考えていきます。
本問は与えられた関数がxの4次関数ですから, そのまま最小値を求めるのは難しいですね。
よって,
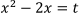
とおくことで与式をtの2次関数ととらえ, その最小値を求める問題と置き換えて考えるのが得策です。
2次関数であればグラフを簡単にかけるので, それを利用して最小値を求められるからです。
ところで置き換えた後の関数
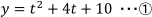
はすべての実数tについて定義されている関数でしょうか?
tは任意のxに対して
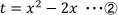
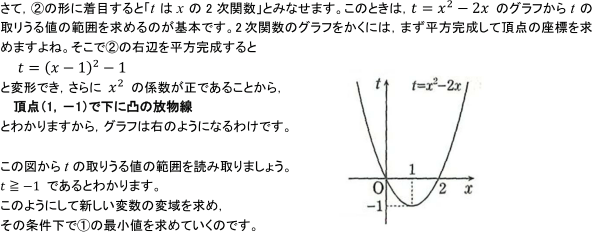
により定義される値ですから, xが全ての実数をとるときtがどの値をとり得るか調べなければ, 関数①の定義域はわかりませんね。
よって, 「置き換えたら新しい変数のとり得る値の範囲をチェックする」必要があるのです。
【学習アドバイス】
変数を置き換えることで問題を簡単に考える手法はよく使われるものです。このときに忘れてはならないのは「新しい変数の変域をチェックする」「新旧変数の対応関係を確認する」「置き換えたことにより問題をどう読み換えて解いていくか整理する」ことです。記述式の問題では, これらを答案上にきちんと示しておくことも大切ですよ。
今後も『進研ゼミ高校講座』を活用して得点アップを目指しましょう。
















