【2次関数】2次方程式の解の存在範囲と判別式
二次方程式x^2-4ax+a+2=0 の2つの解(重解も含む)がともに正であるときの条件は
判別式が0 以上
軸が正
f(0)が正
なんですけど,判別式を示さなくても良いときと,判別式を示すときの違いがよく分かりません。
進研ゼミからの回答
こんにちは。頑張って数学の学習に取り組めていますね。
いただいた質問についてさっそく回答いたします。
【質問内容】
【問題】
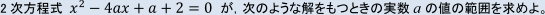
(1)2つの解(重解も含む)がともに正
【解答解説】から抜粋部分

この問題では, 「(判別式)≧0, 軸が正, f(0)>0」を考えますが, 判別式についての条件を考えなくてよい問題もある理由についてですね。
【質問への回答】
2次方程式の解の存在範囲は, 「2次関数のグラフがx軸と交わる部分」に関する問題に置き換えて考えることができます。
のがポイントですね。
グラフを利用して与えられた範囲内に, x軸との共有点が存在する条件を, 視覚的に考えていきます。
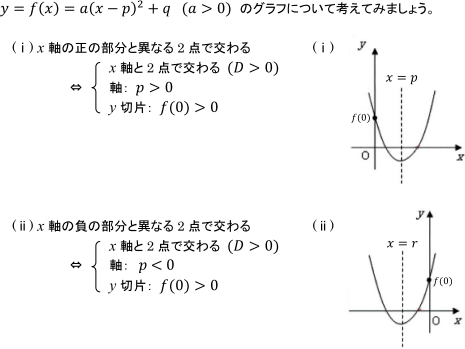
今回の問題の(1)2つの解(重解も含む)がともに正である条件は, 上記の(ⅰ)の場合(ただし, D=0 を含む)となります。
この場合は,

このほか, 次のような場合も考えられます。

境界となるxの値よりも小さい解と大きい解を1つずつもつ場合ですね。
この場合は

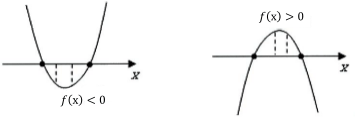
このように, 下に凸の放物線で f(x)<0(y座標が負)となるような部分があればx軸と必ず交わるので, 判別式の条件式は必要ありません。
また, 上に凸の放物線の場合, f(x)> 0(y座標が正)となるような部分があれば, x軸と必ず交わるので, 判別式の条件式は必要ありません。
【学習アドバイス】
判別式について考えなくてよいのは, (ⅲ)のパターンですね。
このような問題では, 2次関数のグラフをかいて, 視覚的に条件を押さえるのが, ポイントです。
条件を整理し, 判別式について, 考える必要がある場合と, そうでない場合とを見極められるようにしておきましょう。
これからも『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。
















