【数と式】因数分解の式変形について
問題の解説のここがわかりません。
3x^2+(y+6)x-(2y-3)(y+1)
={3x-(2y-3)}{x+(y+1)}
詳しい解説をお願いします。
進研ゼミからの回答
こんにちは。
いただいた質問について、早速、回答します。
【質問の確認】
【問題】
次の式を因数分解せよ。
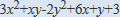
の
【解答解説】からの抜粋部分
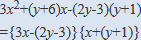
の式変形についてですね。
【解説】
これは、たすきがけの手法の応用ですね。ご質問の式を見てみます。
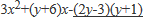

ここで、「たすきがけ」を利用して、xの係数がy+6になる組み合わせを考えてみましょう。
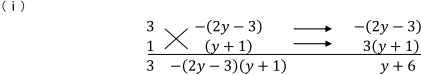
(y+6)は、xの係数になっていますので、この組み合わせが正解です。よって、{3x-(2y-3)}{x+(y+1)}となります。解説にも(ⅰ)に相当する式が書いてありますね。
念のため、他の組み合わせについても確認してみましょう。
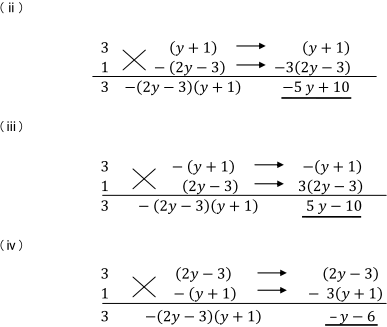

【アドバイス】
複数の文字を含んだ因数分解では1つの文字に注目して整理します。今回のように最後の項が文字式の積の形になる場合は、組み合わせが決まっているので、たすきがけの形にして、xの係数を計算して確認すれば比較的簡単に正しい組み合わせを1個だけ決められます。最初は(ⅰ)~(ⅳ)のように、全ての組み合わせを確認して、確実に正解を見つけ出すようにしましょう。
それではこれで回答を終わります。これからも『進研ゼミ高校講座』で確実に力をつけていってくださいね。
















