【数と式】因数分解のしかた
3x^2+xy-2y^2+6x+y+3=3x^2+(y+6)x-(2y-3)(y+1)
={3x-(2y-3)}{x+(y+1)}
=(3x-2y+3)(x+y+1)
途中式、だいぶはしょっちゃったんですけど…
答えの前の式から答えの式になる流れはわかるのですが、答えの前の前の式から答えの前の式への流れがわかりません。
展開の公式を利用した因数分解ですか?(あ、でも、因数分解は絶対展開の公式を利用しますよね…(^-^;))
私が知りたいのは、上記の式の因数分解の流れです。
どうしてそのようにまとめるのかを教えてください!
進研ゼミからの回答
こんにちは。
いただいた質問について、早速回答します。
【質問の確認】
【問題】
次の式を因数分解せよ。
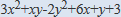
の問題について
【解答解説】
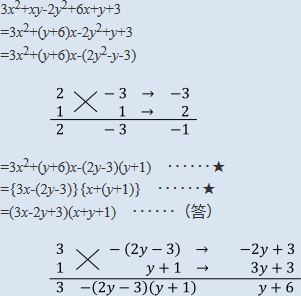
の★の部分の式変形について、ですね。
【解説】
では、わかりやすくする為に、その部分だけを抜き出して、説明しましょう。
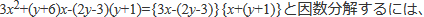
「たすきがけ」を使います。その詳しい手順は、次のようになっています。

さて、③で各2数を配置する際、もし、3と1の上下を逆に配置していたらどうなるでしょう~?
また、②の2数を(2y-3)と-(y+1)のように、-を逆に配置していたらどうなるでしょう~?
これらはいずれも、ad+bcの値がxの係数に一致せず、そのような配置または2数の組み合わせでは駄目なことが分かります。そのような場合は、ad+bcの値がxの係数に一致するa,b,c,dがみつかるまで①~⑥を繰り返し行います。
【アドバイス】
以上で説明を終わりますが、どうでしょう・・分かりましたか?
回答内で挙げた例は、最終的な結果で、そこにたどり着くまでには、何回か①~⑥を繰り返さなければならないかもしれません・・。ぜひ!自分で試してみてくださいね。そして、駄目なパターンを何回も経験して下さい!それによって、たすきがけの手順にも慣れ、身に付いていきますよ。今後も使う重要な因数分解なので、何回も失敗して上手くなっていきましょう!
では、これからも『進研ゼミ高校講座』を大いに活用し、あなたの学習に役立てて下さいね。
















