【数と式】絶対値記号を含む方程式・不等式の解き方
A.|x+3|=4 B. |x+3|=4x C. |x+3|<4 D. |x+3|≧4xの解き方を教えてください。
進研ゼミからの回答
こんにちは。
いただいた質問について,さっそく回答いたします。
【質問の確認】
A.|x+3|=4
B.|x+3|=4x
C.|x+3|<4
D.|x+3|≧4x の解き方を教えてください。
というご質問ですね。
【解説】
≪絶対値記号のはずし方の基本≫
|3|=3,|-3|=-(-3)=3のように,絶対値記号は中身が正か0のときはそのまま,中身が負のときは,中身に「-(マイナス)」をつけ,値が正になるようにしてはずしました。
|x+3|の場合も同じです。ただし,x+3はxの値によって,正にも0にも負にもなるので,場合分けをする必要があるのです。
(ⅰ) 中身が0以上,つまりx+3≧0のとき,すなわちx ≧-3のときは,絶対値記号はそのままはずせて,
|x+3|= x+3
(ⅱ) 中身が負,つまりx+3<0のとき,すなわちx <-3のときは,絶対値記号は中身に「-(マイナス)」をつけてはずすので,
|x+3|= -(x+3) =-x-3
ここまでできれば,あとは普通の方程式や不等式と同じように解くことができます。ただし,絶対値記号をはずしたときの場合分けの条件を満たしているかを最後に確認する必要があるので,注意が必要です。
≪絶対値記号を含む方程式・不等式を解く手順≫

です。この手順に従って解いていきましょう。
【A. |x+3|=4を解く】

【別解】また,絶対値の性質「c>0のとき,|x|=c ⇔ x=±c」を利用すると,次のように解くこともできます。

【B. |x+3|=4xを解く】

【別解】また,絶対値の性質「c>0のとき,|x|=c ⇔ x=±c 」を利用すると,次のように解くこともできます。

【C. |x+3|<4を解く】

【別解】また,絶対値の性質「c>0のとき,|x|<c ⇔-c < x<c 」を利用すると,次のように解くこともできます。
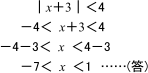
【D. |x+3|≧4 xを解く】

【別解】また,絶対値の性質「c>0のとき,|x|>c ⇔ x <-c , c <x 」を利用すると,次のように解くこともできます。

【アドバイス】
絶対値記号を含む計算でよく利用する絶対値記号のはずし方の基本
a≧0のとき,| a |=a
a<0のとき,| a |=-a
をしっかりと身につけておきましょう。
また,余裕があれば,【別解】で紹介したような絶対値の性質を利用した解き方も理解しておくとよいでしょう。
それでは,これで回答を終わります。
これからも,『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。
















