【数と式】連立不等式の解の求め方
解答にあるように二つの不等式をつくり、正しく解き、①、②の答えは出たのですが、最後の共通範囲の答えがx>5になるのがわかりません。①で求めたx>2はどうして使わないのでしょうか?図を見てもイマイチわかりません…
進研ゼミからの回答
こんにちは。
いただいた質問について、早速、回答します。
【質問の確認】
【問題】
4x-3>2x+1>x+6
の問題について、
【解答解説】

の解答解説にでてくる
「x>2 ・・・①」はなぜ使わないのかというご質問ですね。
【解説】
教材にあるように
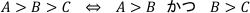
であるので、4x-3>2x+1>x+6の解は
4x-3>2x+1 の解 x>2 ・・・①
2x+1>x+6 の解 x>5 ・・・②
を同時に満たすxの範囲になります。
① ②の範囲を数直線上に示すと
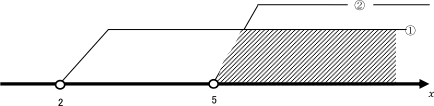
となります。
①かつ②である部分は、①の範囲と②の範囲が重なる部分、つまり斜線の部分になります。
このとき①の 2<x の結果が反映されていないわけではありません。
①の範囲 2<x に②の範囲 5<x を重ねると 5<x になるという意味です。
具体的な数値で考えると、x=3 は 2<x を満たしていますが、5<x には含まれませんね。
「2<x かつ 5<x 」であるxの値の範囲は、5<x となります。
5<x の範囲はすべて 2<x を満たしているのは明らかです。
【アドバイス】
連立不等式の解は、それぞれの不等式の解の範囲を数直線で表し、それらの共通範囲を求めます。「3<xかつ x<5の共通範囲は3<x<5」のように2つの値に挟まれる場合はわかりやすいのですが、今回のように「2<x かつ 5<x 」のように不等号の向きが同じ場合は注意が必要です。
数直線の見方をしっかりマスターしましょう。
それでは、これで回答を終わります。
これからも『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。
















