【数と式】「pならばq 」が真のとき,集合Pが集合Qに含まれる理由
条件pを満たすもの全体の集合をP ,条件q を満たすもの全体の集合Qとするとき,「 p ⇒q 」が真であるときに P⊂Qが成り立つのか,P⊃Qが成り立つのかわかりません。
進研ゼミからの回答
こんにちは。
いただいた質問について,さっそく回答いたします。
【質問の確認】
条件pを満たすもの全体の集合をP ,条件q を満たすもの全体の集合Qとするとき,「 p ⇒q 」が真であるときに P⊂Qが成り立つのか,P⊃Qが成り立つのかわかりません。
というご質問ですね。
【解説】
・「 p ⇒q 」が真であるということ
・⊂,⊃の記号の使い方,すなわち,集合の包含関係
を理解すれば,わかるようになります。
「命題の真偽」と「集合の包含関係」は,一見違うことに思われますが,実は同じことなのです。
集合のベン図をかくことによって,このことを考えてみましょう。
≪命題の真偽をベン図に表す≫
まず,命題の真偽について確認しましょう。
【命題とその真偽】
正しいか正しくないかが明確に決まる式や文章を命題という。
命題が正しいとき,その命題は真であるといい,正しくないとき,その命題は偽であるという。
「 p ⇒q 」が真,つまり「 p ⇒q 」が成り立つ,ということをベン図に表してみましょう。
条件pを満たすもの全体の集合をP,条件qを満たすもの全体の集合をQとすると,Pに含まれているものx は,条件pを満たしています。今,「 p ⇒q 」が成り立っているのですから,xは条件qも満たしているということになり,xはQに含まれるのです。
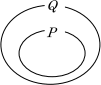
つまり,Pに含まれているものはすべて,Qに含まれることになり,このことを集合のベン図で表すと,図1のようになります。

≪包含関係をベン図で表す≫
集合のベン図と⊂,⊃の記号の関係を確認しましょう。

すなわち,(含まれる方)⊂(含む方)となります。
よって,図1より,「 p ⇒q 」が真である,ということは,P⊂Qであるということそのものであることがわかります。
【例1】
命題「4の倍数⇒2の倍数」は真なので,(4の倍数全体の集合)⊂(2の倍数全体の集合)となっています。


★まとめ★
条件pを満たすもの全体の集合をP,条件qを満たすもの全体の集合Qとするとき,
「 p ⇒q 」が真⇔P⊂Q
となります。
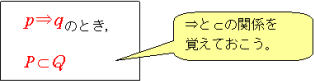
【アドバイス】
「 p ⇒q 」が真 のとき P⊂Qにおいて,⇒と⊂の関係を覚えておきましょう。
このとき,下のような集合のベン図をかいてPからどんな要素をとっても,それはQの要素になる,すなわち, P⊂Qとなると理解しておくとよいでしょう。
それでは,これで回答を終わります。
これからも,『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。
















