【数列】a_(n+1)=pa_n+q (p≠1,q≠0)型の漸化式の解き方
講義の例題で数列{an}が漸化式 a1=3,an+1=3an-4 を満たしているとき、なぜα と置いてα =3α -4 になるのですか?
an と、an+1 がまるで等しいかのように…
本当にわかりません。
進研ゼミからの回答
こんにちは。
いただいた質問について、早速、回答します。

について、②の部分が成り立つ理由についてですね。
【質問への回答】
《理由について》

《例題で練習》

【アドバイス】
以上で説明を終わりますが、どうでしょう・・分かりましたか?
数列の漸化式から一般項を求める方法は、各漸化式によって決まっています。種類も多く、覚えるのも大変ですが、逆に覚えていないと解けないので、しっかり覚えておきましょう。
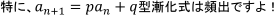
求める手順は前述の4つ(①~④)!今回を機に、しっかり習得してくださいね!
ではこれからも『進研ゼミ 高校講座』を大いに活用し、あなたの学習に役立てて下さいね。
















