【数列】格子点の個数について
別解では平行四辺形を使って格子点の個数を求めていますが
対角線AC上の格子点の個数がどうしてn+1(個)になるのでしょうか?
進研ゼミからの回答
こんにちは。
がんばって数学の勉強に取り組んでいますね。質問をいただいたのでお答えします。
【質問内容】
【問題】
n は自然数とする。座標平面上の3点(0,0)、(3n,0)、(2n,n)を頂点にもつ三角形の周および内部に含まれる格子点(x座標 y座標がともに整数である点)の個数を求めよ。
【解答解説】から抜粋部分

【解答解説】のように平方四辺形を使って格子点を求めたとき、(★)部で(n+1)個となる理由ですね。
【質問への解答】
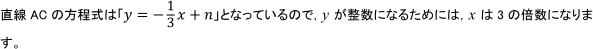
これにより、線分AC上にある格子点を順に挙げていくと次のようになります。
A(0,n),(3n-1),(6,n-2),・・・・・・,(3n-3,1),C(3n,0)
これらy座標に注目すると「n,n-1,n-2,・・・,1,0」となっていて、この個数が「線分AC上にある格子点の個数」になるので、
(線分AC上にある格子点の個数)=(0からnまでの整数の個数)=n-0+1=n+1(個)
となっています。
【学習アドバイス】
「格子点」というのは、「x座標,y座標がともに整数になる点」のことなので、線分AC上にある格子点を順に 挙げていってその個数を調べていきましょう。
「(0からnまでの整数の個数)=n+1(個)」となることもよく理解しておきましょう。
では、この調子でがんばってゼミの教材の問題に取り組み、実戦力を養っていってくださいね。
応援しています!
















