【整数の性質】余りを用いた整数の分類について
n^2を4で割ったときの余りを考えるとき,なぜnを4で割ったときの余りで分類するのですか?
進研ゼミからの回答
こんにちは。
では, 早速, 質問にお答えしましょう。
【質問内容】
【問題】
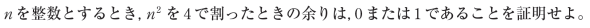
【解答解説】から抜粋部分

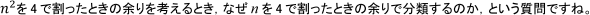
【質問への回答】
ここで説明したいことは, 「4で割った余り」に関することですね。
だから, 整数全体を4で割った余りで分類して考えるのです。
整数には, 次の基本的な性質があります。
整数全体は, 整数 p(p>0) で割ったときの余り, 0, 1, ……, p-1 によって p 通りに分類できる
つまり整数を4で割った余りは0か1か2か3なので, 整数nは必ずこれらの4通りのどれかになります。
それを表したのが, kを整数とした次の式です。
n=4k+0 ← 余りが0で, 4で割り切れる整数です。
n=4k+1 ← 4で割ると1余る整数です。
n=4k+2 ← 4で割ると2余る整数です。
n=4k+3 ← 4で割ると3余る整数です。
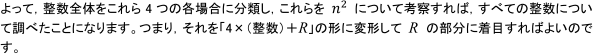
上記4通りにおいて, Rが1か0しかなければ, 題意が証明されたことになりますね。
以上のように, まずは, 「元になる数 n」を4で割った余りで分類し, 与えられた式「n の2乗」について考えて
いくのです。
【学習アドバイス】
このような問題が出たら, 迷うことなく整数全体を分類できるよう, 解法の流れをしっかり確認して
おきましょう。
では、これからも『進研ゼミ 高校講座』を大いに活用し, あなたの学習に役立ててくださいね!
















