【整数の性質】方程式を満たす1組の整数解を求める途中の式変形について
1=17-(25-17・1)・2
=17-25・2+17・2
=25・(-2)+17・3
とありますが,なぜ
17-25・2+17・2から25・(-2)+17・3と変形できるのかわかりません。
解説お願いします!
進研ゼミからの回答
こんにちは。
では,いただいた質問にお答えしていきましょう。
【質問の確認】
【問題】
等式 25x+17y=1を満たす整数x,yの組を1つ求めよ。
【解答解説】から抜粋部分

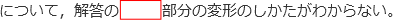
というご質問ですね。
【解説】
「互除法」を使って,
25=17・1+8
17=8・2+1
となることより,
1 =17-25・2+17・2 …☆
となるところまでは変形できたのですね。
これより,☆の右辺を25・■+17・● の形にしますが,
25を因数にもつ項,17を因数にもつ項をそれぞれ同類項としてまとめていく
のがポイントです。
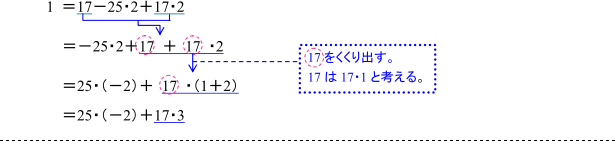
下線部分をもう少し詳しく説明しましょう。
17と17・2は同類項なので,次のようにまとめています。
17+17・2=17・1+17・2
=17・(1+2)
=17・3
また,-25・2は,25の符号を“+”にするために,
-25・2=(-25)×2
=25×(-2)
=25・(-2)
と変形しています。
【アドバイス】
1組の整数解を求めるときに,例えば,8x+3y=2 なら,
すぐに,x=1,y=-2 とわかります。
このように,簡単な数値を代入してみてすぐにわかるときはよいのですが,すぐにわからなければこの問題のように,互除法を利用します。
それでは,これで回答を終わります。これからも『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。
















