【振動数条件】原子の分野でエネルギーがとびとびの値しかとれないのはなぜ?
「hv」のvをいろいろ変えれば,エネルギーはどんな値でもとることができるのではないのですか?
進研ゼミからの回答
【質問内容】

《原子の分野では,エネルギーがとびとびの値しかとれないというのはどういう意味ですか。》
「hv」のvをいろいろ変えれば,エネルギーはどんな値でもとることができるのではないのですか?
【質問への回答】
●「原子のエネルギーがとびとびの値しかとれない」理由は,ボーアの理論で説明されます。
波である光が,光子という粒子のように振る舞うのと同じように,粒子である電子も,波のような性質をもっています。
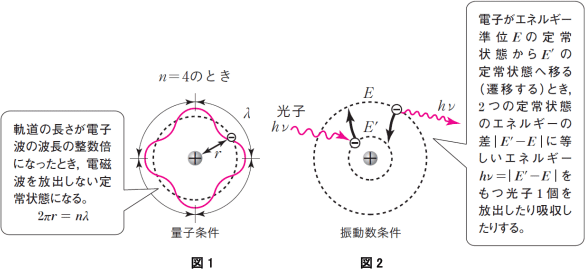
原子核のまわりを回転している電子は,光子を放出してエネルギーが小さくなると,軌道半径が小さくなります。ここで,エネルギーがだんだん小さくなっていっても原子核に衝突してしまわないためには,電子が軌道上で定常波(定在波)をつくって定常状態になっていることが必要だとボーアは考えました(図1参照)。
●水素原子の例で,定常状態となる状況を考えてみましょう。
水素の原子核(電気量+e)のまわりを質量mの電子(電気量-e)が等速円運動している状況を考えます。
電子の円運動の速さをv,軌道半径をr,クーロンの法則の比例定数をkとすると,静電気力が向心力となるので,中心方向の運動方程式は

n以外はすべて定数なので,定常状態になるとき,電子の軌道半径rはnの値によって決まる,とびとびの値をとることがわかります。
●このことから,エネルギーもとびとびの値になるかを確かめてみましよう。
先ほど求めた軌道半径rを用いて,水素原子内の電子がもつエネルギーを求めてみます。無限遠を基準としたときの静電気力による位置エネルギーUは
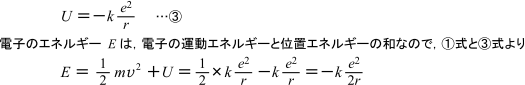
となります。軌道半径rはnによって決まるとびとびの値なので,電子のエネルギーEもとびとびの値をとることが確認できました。
●「hv」は,振動数条件を表しています。
振動数条件とは,
「電子エネルギーEの状態から,それよりも低いE'の状態に移動するとき,E-E'=hvで表されるエネルギーhvの光子を放出する。」
ということでしたね(図2参照)。
式だけを見ているとvはいろいろな値をとることができるように思えますが,上の水素原子の例で見たように,原子がもつことのできるエネルギーの状態は決まっているので,電子がそのエネルギー状態間を移動して放出する光子の振動数vも,原子によって決まってきます。このとき出てきた光は,線スペクトルとよばれます。
例えば,高速道路のトンネルなどに使われているオレンジ色の明かりはナトリウム灯といいます。ナトリウム灯は,ナトリウムに独特の,オレンジ色の波長の光子を放出しています。
このように,ある原子によって放出される光子は,特定の波長(振動数)のものだけとなります。それは,E,E’がとびとびの値なので,hvもとびとびの値しかとれないからなのです。
【学習アドバイス】
「電子は振動数vの光を放出するのに,軌道半径がどんどん小さくなって原子核に衝突してしまわないのはなぜか。」という疑問を解消するために,ボーアの理論が立てられました。その理論をもとに様々な計算を行ってみると,実際に観測される現象を正確に説明できることがわかったのです。












