単振動の運動方程式 なぜマイナスがつくの?
単振動の運動方程式は,ma=-Kxとなっているけれど,なぜマイナスがつくのですか。
ばねなのに,フックの法則のF=kxとは違うのですか。
進研ゼミからの回答
【質問内容】
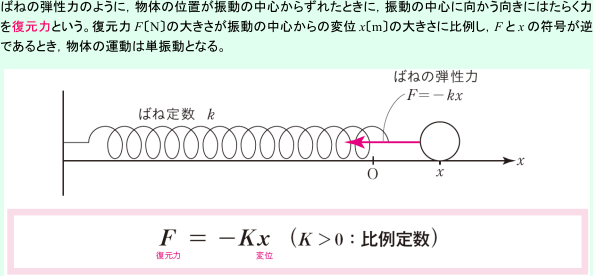
《単振動の運動方程式は,なぜマイナスがつくのですか。》
単振動の運動方程式は,ma=-Kxとなっているけれど,なぜマイナスがつくのですか。
ばねなのに,フックの法則のF=kxとは違うのですか。
【質問への回答】
運動方程式:ma=-Kxと,フックの法則:F=kxでは,xの意味が違います。
単振動の運動方程式:ma=-Kxのxは,原点(振動中心)からの位置の変化で,正負がありますが,フックの法則は,弾性力の大きさを表す式なので,F=kxのxは,ばねの自然長からの伸び,または縮みとなり,正の値のみになります。
まず,運動方程式について確認しましょう。
運動方程式:ma=Fとは,
「質量mの物体に加速度aが生じるとき,物体にはたらく力はFである」
あるいは「質量mの物体に力Fがはたらくとき,加速度aを生じる」
aとFの正の向きを同じにして立てる。
フックの法則:F=kxは弾性力の大きさを求める式ですから,運動方程式とは意味が違うことがわかりますね。
続いて図のように,ばね振り子をなめらかな水平面上に置き,一端を壁に固定した水平方向のばね振り子の運動方程式について考えてみましょう。
ばねの自然長の位置(ここでは振動中心)を原点Oとして,図のようにx軸をとります。
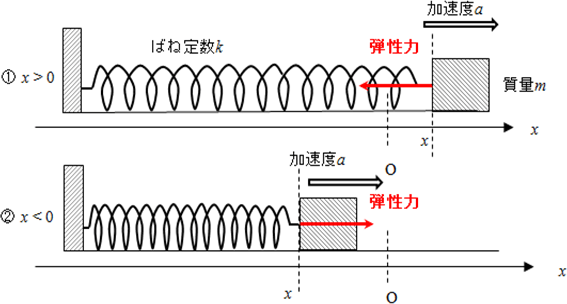
①のようにx>0の場合,ばねの伸びはx(>0)ですから,フックの法則より,弾性力の大きさはkxです。加速度の正の向きをx方向正の向きにすると,弾性力はx方向負の向きにはたらいていますから,運動方程式は,ma=-kxとなります。
②のようにx<0の場合,ばねの縮みは|x|=-x(>0)となりますから,弾性力の大きさは,k|x|=-kxです。弾性力がはたらく向きは,x方向正の向きですから,運動方程式は,ma=k|x|=-kxとなり,①の場合と同じになります。
③x=0のときは,弾性力も0ですから,加速度も0となり,運動方程式:ma=-kxに含まれます。
よって,xが正であっても負であっても,ばね振り子の運動方程式はma=-kxとなり,右辺にマイナスがつきます。この右辺の-kxは,常に中心:x=0に向かう力なので,復元力(元に戻す力という意味)といいます。
【学習アドバイス】
単振動の運動方程式:ma=-Kxは,質量mの物体に加速度aを生じさせる力が変位xに比例する復元力:-Kxであるということを意味しています。(Kは比例定数で正の値)。
水平方向のばね振り子の場合は,K=k(ばね定数)となります。
運動方程式が,ma=-Kxで表される運動は,すべて単振動をしているといえます。












