【地球の概観と構造】エラトステネスの方法について
この問題がまったくわからず,解説を読んでも理解できませんでした。
エラトステネスの方法について,もっと具体的に,わかりやすくおしえて下さい。
進研ゼミからの回答
こんにちは。 さっそく質問に回答しますね。
【質問内容】
【問題】
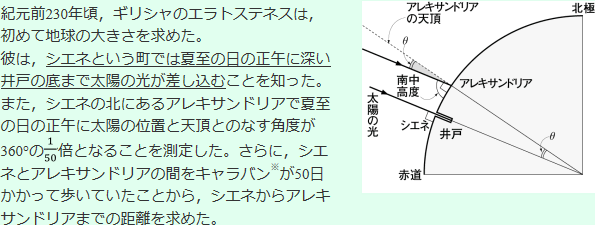
以上の値を利用して,地球が完全な球であるとすれば,地球の全周は[ A ]km,半径は[ B ]km と計算することができた。
※キャラバンとは,らくだに荷物を載せて隊列を組んで行商する隊商のことである。
[ A ],[ B ]に入る数値を求めよ。ただし,円周率π = 3.14 とし,有効数字2桁で答えよ。
という問題について,
【解答解説】
夏至の日の正午に,シエネでは天頂に見える太陽が,アレキサンドリアでは天頂から
![360°×1/50=7.2°ずれているということなので、問題の図で両地点の緯度差θ=7.2°である。地球の全周をL[km]とすると、L:925km=360°:7.2° よって、L=925×360/7.2=46250≒4600[km] 地球の半径をR[km]とするとL=2πR=46250kmだからR=46250/(2×3.14)≒7400[km]](/teikitest/_resource/img/kou/science/k_sc_378_2.png)
の解説を,もっと詳しく教えてほしい,というご質問ですね。エラトステネスの方法について,一緒にみていきましょう。
【質問への回答】
エラトステネスは,地球が球形であると仮定し,エジプトのアレキサンドリアとそのほぼ真南にあるシエネの間の距離と緯度の差を測定して,地球の周囲の長さを求めました。
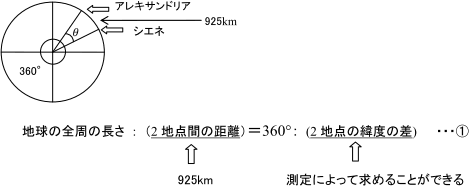
アレキサンドリアとシエネの間の距離は,前の設問で求めていて,925kmとわかっていますから,緯度の差をどのように求めたのかを解説します。
[アレキサンドリアとシエネの緯度の差]
天頂と太陽の光の方向について確認しておきましょう。
天頂は,それぞれの地点の真上を指しています。(地表面と垂直な方向)
太陽は非常に遠方にあるので,太陽の光の方向は平行光線と考えることができます。
シエネでは,夏至の日の正午に太陽が真上から照らしていることを,井戸の水面に太陽がうつることで知りました。
これより,シエネでは,夏至の日の正午の太陽の光の方向と,天頂は一致していることがわかります。
アレキサンドリアでは,夏至の日に正午の太陽の方向と,天頂のなす角を測定したら360°の

です。
よって,この2地点の緯度の差は,7.2°とわかります。
下の図を参考にしてください。
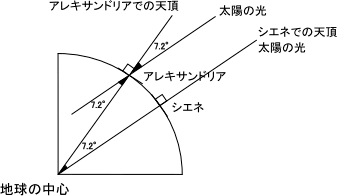
よって,①の式に,2地点の緯度の差7.2°を代入して,地球の全周の長さを求めることができます。
エラトステネスの方法は「地球が球である」という仮定のもとに行われています。
実際には地球は回転楕円体に近い形です。シエネとアレキサンドリア間の距離も正確とはいえません。
ほかにも正確でない点がいくつかあり,この方法で計算された地球の全周は,実際の約40000kmとは一致しません。
とはいえ紀元前230年に地球の大きさを計算して求めた数値だということを考えれば,かなり近い数値を出しているといえるのではないでしょうか。
【学習のアドバイス】
初めて地球の全周の長さを求めた方法として,エラトステネスの方法はよく出題されます。
どのように考えたのかを正確に理解しておきましょう。
今後も『進研ゼミ高校講座』を使って,得点を伸ばしていってくださいね。












