【確率分布】確率密度関数
問題の解き方はわかるんですけど,どうして,確率が面積になるのかちょっと理解できていないと思います。
講義に,「確率密度関数自身は確率を表すのではない」とあって,わからなくなりました。
今まで,確率は面積じゃなかったのに,どうして面積なんですか?
進研ゼミからの回答
こんにちは。
いただいた質問について、早速、回答します。
【質問内容】
【問題】

【解答解説】から抜粋部分
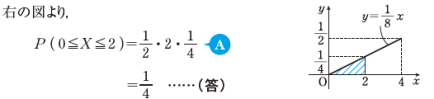
上のように、確率変数 Xの確率密度関数がわかっているとき、確率が面積で求められることが理解できないというご質問ですね。
【質問への回答】
例えば、1個のさいころを投げて出る目(1,2,3,4,5,6)のように、とびとびの値をとる確率変数に対して、長や体重のように連続した値をとる確率変数を考えてみましょう。
《連続した値をとる確率変数》
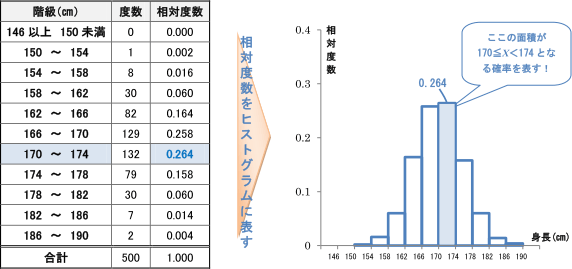
ある高校の2年男子の身長を測定した結果を整理して、次のような度数分布表が得られたとします。
この中から1人を選んで、その身長を Xとするとき、170≦X≦174の階級に属する確率は、相対度数 0.264 と考えられます。
そして、右下のように、各階級の上の青色の長方形の部分の面積がその階級の相対度数を表すようにヒス トグラムをかきます。
このように考えると、Xがある階級に存在している確率は、ヒストグラムの面積で表されると言えるのです。

以上のことをー般的にまとめておきましょう。

このような曲線を、分布曲線といいます。
そして、Xの分布曲線の方程式を y=f(x)としたときのf(x)を確率密度関数といい。関数の値が確率を表すのではなく、確率は面積で表されます。
したがって、

ということを示しているのです。
【学習アドバイス】
今回は、確率密度関数から確率を求める問題でした。
確率密度関数とは、
・Xに1つの曲線を対応させて、
・a≦X≦bとなる確率が、図の斜線部分の面積を表されるようにしていること
が、ポイントです。定義を頭にいれて、問題に取り組みながら使い方を身につけていきましょう。
今後も『進研ゼミ高校講座』を使って、積極的に学習を進めてください。
















