【確率分布】標準正規分布に従うときの確率の求め方
P(-0.8<Z≦1.6)の確率を求めるときに,不等号に等号がついていなくても同様に考える,と書いてありました。
どうしてですか?
等号がついていてもいなくても同じ,と考える理由がわかりません。
進研ゼミからの回答
こんにちは。
いただいた質問について、早速、回答します。
【質問内容】
【問題】
確率変動Zが標準正規分布N(0,1)に従うとき、正規分布表を利用して、次の確率を求めよ。
P(-0.8<Z≦1.6)
上のように、P(-0.8<Z≦1.6)と不等号に等号がついていないときの確率を求めるときに、等号がついているときと同様に考える理由がわからない、というご質問ですね。
【質問への回答】

を計算することになります。
このときのP(0≦Z<0.8)は0.8は含まない(等号がついていない)のですが、
P(Z=0.8)を考えたとき、
この値は、P(0.8≦Z≦0.8)と考えることができる。
そして、P(0.8≦Z≦0.8)=0 となることから、
P(Z=0.8)=0 …★ と言える。
P(0=0.8)には、区間の幅がないので、面積を考えることが
できない。だから、P(Z=0.8)=0 と考えても良い。
このことから
P(0≦Z<0.8)=P(0≦Z≦0.8)
と考えてもよい、としているのです。
《上記の★について》
確率変動Xが連続型確率変数のとき、すなわち、Xがある範囲の実数値のすべてをとりうるときに、実数aをとる確率P(X=a)とは…
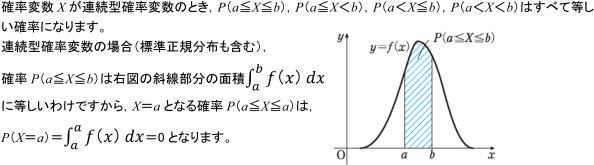
このように連続した値をとる確率変数では、確率変数がある範囲にあるときの確率を考えます。
【学習アドバイス】
不等式に等号がつくか、つかないか、意識しながら学習を進めているのはよいことですね。
今回のような、正規分布表を用いた確率の問題では、等号の有無に左右されずに、どこの面積に、どの確率が表れているか…ということを意識して計算をしていくとよいですね。
今後も『進研ゼミ高校講座』を使って、積極的に学習を進めてください。
















