【空間ベクトル】垂直であることの証明の仕方
「正四面体ABCDにおいて,△BCDの重心をGとすると,AG⊥BCである。このことを,ベクトルを用いて証明せよ。」という問題の考え方がわかりません。
進研ゼミからの回答
こんにちは。
いただいた質問について、早速、回答いたします。
【質問内容】
【問題】
正四面体ABCDにおいて,△BCDの重心をGとすると,AG⊥BCである。このことを,ベクトルを用いて証明せよ。
という問題の証明の仕方がわかりません。
というご質問ですね。
【質問への回答】
まず、問題の整理をしてみましょう。
【ポイント1】問われていることに注目!
この問題で問われているのは、「ベクトルを用いて、垂直であることを示すこと」だから…
垂直を、(ベクトルの内積)=0ととらえる。
つまり、
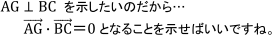
【ポイント2】証明で用いる基本となる3つのベクトルを決める!
最も一般的な3つのベクトルは、
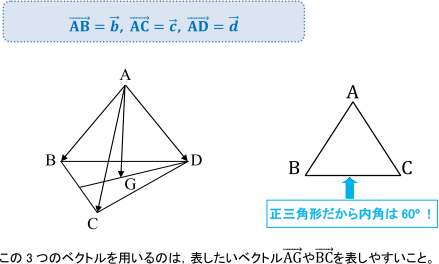
また、この3つのベクトル同士の内積や大きさの関係が簡単にわかるからです。
つまり、

【ポイント3】 問題文から、使える条件を考える!
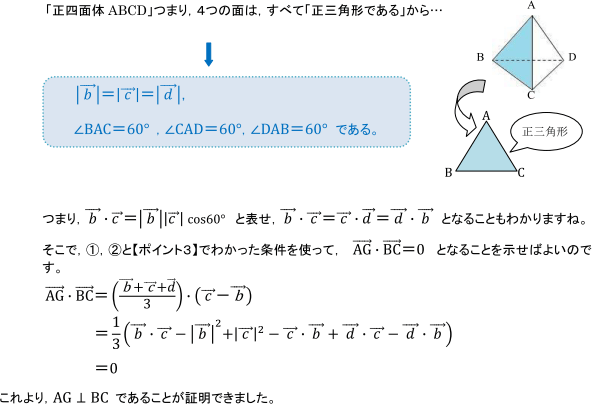
【学習アドバイス】
「垂直」ときたら、「(内積)=0」を思い浮かべることがポイントでした。
三角形の重心の表し方を確認し、「正四面体」という図形的な特徴にも注目して、基本となる3つのベクトル を設定して、内積を計算してみることから始めましょう。
示すべき式を頭に置いて、計算を進めてみるとよいですね。
今後も、わからないところは早めに解決しながら、数学に取り組んでいってくださいね。
















