【場合の数と確率】確率の使い分け
確率を求めるとき条件つき確率なのか,独立試行の確率なのか,反復試行の確率なのか,乗法定理なのか・・・どのように文章から見分けるのかわからないので教えてください。
進研ゼミからの回答
こんにちは。
いただいたご質問について, 回答いたしますね。
【質問内容】
確率を求めるとき条件つき確率なのか, 独立試行の確率なのか, 反復試行の確率なのか, 乗法定理なの
か…どのように文章から見分けるのかわからないので教えてください,
というご質問ですね。
【質問への回答】
まず, ご質問のそれぞれの定義を確認しておきましょう。
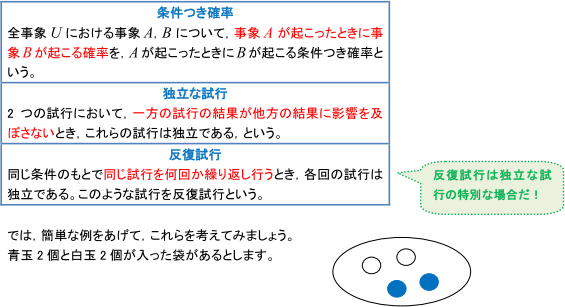
① 袋から玉を1個取り出し, 取り出した玉をもとに戻してもう1個取り出すとき
玉を取り出す1回目の試行と, 2回目の試行は互いの結果に影響を及ぼさない
⇒これらの2つは独立な試行である。
② 袋から玉を1個取り出してもとに戻す, という試行を5回行うとき
袋から玉を取り出す同じ試行を5回繰り返す
⇒反復試行
③ 袋から青玉を1個取り出した。その後, 取り出した青玉を戻さないで, 白玉を1個取り出すときの確率
袋から青玉を取り出すという事象Aが起こったときに, 白玉を取り出すという事象Bが起こる
⇒条件つき確率
③の確率を求めると, 次のようになります。
A:1個目に青玉が出る B:2個目に白玉が出る
とする。

また,
「袋から玉を1個取り出し, もとに戻さないでもう1個取り出す。1個目で青玉, 2個目で白玉を取り出す確率」
を求める場合, 事象A, Bを③で定めた事象とすると, A, Bがともに起こる確率P(A∩B)を求めることになり
ます。このときは, 「乗法定理」を利用し,
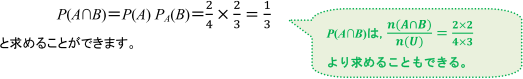
【学習アドバイス】
実際の問題文において, 「このフレーズがあったらこの試行!」といったような判断をするのではなく, 問題文
から, 上記のどの試行にあてはまるのかを, その内容からしっかり判断するカをつけていかなくてはいけま
せん。
それには, その状況をしっかりイメージする力をつけましょう。慣れるまでは具体的に図をかいてみたり, 具
体例などを数例書き出してみるとよいですね。
これからも, 『進研ゼミ高校講座』の教材を利用して, 理解を深めていきましょう。
















