【場合の数と確率】区別がない組分け
①A,B,Cの区別を無くした場合になぜ、同じものとなる分け方がA,B,Cの順列の総数の3!になるのかがわかりません。
②なぜ、A,B,Cの区別したものを、A,B,Cの順列の総数で割るのかもわかりません。
①は図つきで説明してもらえると、大変助かります。
進研ゼミからの回答
こんにちは。
いただいた質問について、早速、回答します。
【質問の確認】
【問題】
12人の作家の本が1冊ずつ計12冊ある。この12冊の本を次のように分ける方法は何通りあるか。
(1) Aさん、Bさん、Cさんに4冊ずつ分ける。
(2)4冊ずつ3組に分ける。
の(2)での
【解答解説】
A,B,Cの3組に区別できるとすると,4冊ずつ3組に分ける分け方は,(1)の結果より,34650通り。
A,B,Cの区別をなくすと,同じものとなる分け方は,A,B,Cの順列の総数,つまり,3!通りずつ
出てくる。
よって,求める分け方の総数は,
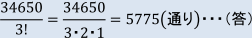
について、
①A,B,Cの区別を無くした場合になぜ、同じものとなる分け方がA,B,Cの順列の総数の3!になるのかがわかりません。
②なぜ、A,B,Cの区別したものを、A,B,Cの順列の総数で割るのかもわかりません。
というご質問ですね。
【解説】
≪具体例を考えてみましょう≫
12冊の本を、①,②,③,④,⑤,⑥,⑦,⑧,⑨,⑩,⑪,⑫とします。
この12冊を3組に分けた例として以下のある1つの組分けの例について考えてみましょう。
{①,②,③,④} {⑤,⑥,⑦,⑧} {⑨,⑩,⑪,⑫}
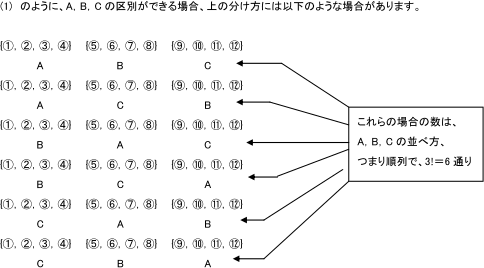
(2)では、A,B,Cの区別がないので、上の6通りの分け方はすべて同じになり、1通りと数えられます。以上より、①~⑫を3つの組に分ける方法の総数をxとすると、x×3!が(1)で得られた分け方の総数に等しくなります。A,B,Cの区別がない場合には、①~⑫を3つの組に分ける方法の総数xがそのまま答えになりますので、(1)の答えを3!で割ることで、3つの組に分ける方法の総数xが求められます。
【アドバイス】
本問は典型的な組分けの問題です。組分けの問題は、(1)のように分けるグループが区別できる場合と、(2)のように区別できない場合とで、計算が異なります。グループの区別ができない場合には、区別ができる場合の分け方の総数を、グループの数nの順列n!で割ることで求められることを覚えておいても良いでしょう。混乱した場合には、上記のように具体的に、ある一例を考えて、区別ができる場合と区別ができない場合の違いを確認しながら進めると良いですね。
それではこれで回答を終わります。これからも『進研ゼミ高校講座』で確実に力をつけていってくださいね。
















