【場合の数と確率】余事象を使った解き方
2本以上当たるのであれば1本当たるではいかないという余事象を使って解いたら1/2が答えになります。
これではだめなのですか
進研ゼミからの回答
こんにちは。
さっそくご質問にお答えしましょう。
【質問の確認】
【問題】
10本のくじの中に、当たりくじが4本入っている。この中から同時に3本のくじを引くとき、2本以上当たる確率を求めよ。
について、余事象を使った解き方についてですね。
(2本以上当たる確率)=1-(1本当たる確率)
と考えたのですね。
【解説】
それだと確かに『1本当たり』の場合の確率を求めてみると
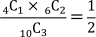
となることから、余事象の確率を用いて

しかし『2本以上当たる』ということの余事象は
本当に『1本当たる』だけでしょうか?
そうですね、『まったく当たらない』つまり『0本当たる』ことも
『2本以上当たる』ことの余事象に含まれます。
よって、『0本当たる』つまり、『全く当たらない』場合の確率
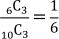
も求めて、「2本以上当たる場合」の確率は
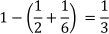
と求めなければならないわけです。
【アドバイス】
このように『○本当たる』ということの余事象には
『1本も当たらない』ということも含まれます。
これは見落としがちなので、今後気をつけるようにしましょう!
















