数学A 定期テスト対策【場合の数と確率】和の法則と積の法則の使い分け

進研ゼミからの回答

こんにちは。
いただいた質問について，さっそく回答いたします。

【質問の確認】

問題を解くときに，和の法則・積の法則のどちらを使ったらよいのか，まったくわかりません。
というご質問ですね。

【解説】

基本的に，「和の法則，積の法則のどちらを使うのか」と，考えることはやめましょう！
問題の状況を考えて，＋，×の使い分けを考えるようにする方が，簡単です。

≪和の法則，積の法則を確認≫
念のため2つの法則を確認しておきます。

【和の法則】
事柄A，Bが同時には起こらないとき，Aの起こり方がm通り，Bの起こり方がn通りとすると，AまたはBのどちらかが起こる場合の数は，（m+n ）通りである。

【積の法則】
事柄Aの起こり方がm通りあり，その各々に対して事柄Bの起こり方がn通りあるとき，AとBがともに起こる場合の数は（ m×n ）通りである。

もう少し簡単な考え方としては，

です。
では例を見ながら押さえていきましょう。

【解答１：数え上げる方法】
まず，すべての行き方を，数え上げてみると，

・A→Bを飛行機，B→Dを飛行機
・A→Bを飛行機，B→Dを船
・A→Bを船，B→Dを飛行機
・A→Bを船，B→Dを船
・A→Cを飛行機，C→Dを飛行機
・A→Cを飛行機，C→Dを船
・A→Cを飛行機，C→Dを新幹線
となり，答えは７通りとなります。

では，今度は違う解き方をしてみましょう。

【解答２：「和の法則」「積の法則」を使う方法】
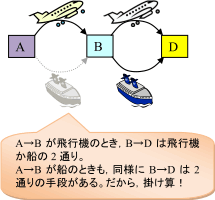
AからDまでの経路は，
(１)A→B→D
(２)A→C→D
という大きく２つの経路があります。そこで，この2つについて別々に考えてみます。

(１) A→B→D
この経路は，さらに，A→B，B→D に分けて考えられます。
(ⅰ)A→Bの経路
この間の経路は，飛行機または船の2通りです。

(ⅱ)B→Dの経路
(ⅰ)と同様に，飛行機または船の2通りです。

A→B→D の経路では，(i)の各々に対して，(ii)の起こり方は2通りあります。 よって，(ⅰ)かつ(ⅱ)より，A→B→D の経路は，


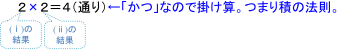
同様に，(２)の経路について，見てみます。
(２) A→C→D
(ⅰ)A→Cの経路
飛行機の１通り。

(ⅱ)C→Dの経路
飛行機または船または新幹線の3通りです。

【解答１】のように数え上げるよりは，【解答２】のように2×2＋1×3と計算をしていく方が効率よく場合の数を求めることができます。
その際，状況を「かつ」「または」で判断していくと，自然に＋，×の使い分けができてくるようになるでしょう。

【アドバイス】

和の法則では，「事柄A，Bが同時には起こらないとき……AまたはBのどちらかが起こる場合の数」， 積の法則では，「AとBがともに起こる場合の数」という条件がポイントになります。問題の状況を考えてどちらの条件に当てはまるかを判断できるようにしておきましょう。いろいろな問題を解くと，それぞれを使い分けるポイントがつかめると思いますので，頑張って挑戦してください。

それでは，これで回答を終わります。
これからも，『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。