【場合の数と確率】確率の乗法定理について
P_A(B)=3/7の時点で答えは出ているのにその下の段でもう一度求めている意味がわかりません。
P_A(B)にP(A)を掛けるというのは不要ではないんですか??
お願いします。
進研ゼミからの回答
こんにちは。ゼミ教材を利用して日々の学習に取り組んでいますね。
では, いただいたご質問にお答えいたしましょう。
【質問内容】
【問題】
8本のくじの中に3本の当たりくじがある。a, bの2人が, 引いたくじをもとに戻さないで, a, bの順に1本ず
つくじを引くとき, aがはずれ, bが当たる確率を求めよ。
【解答解説】から抜粋部分

というご質問ですね。
【質問への回答】
ここで求めたい確率は, 「a がはずれ, b が当たる確率」です。
例えば, 「aがはずれたときに, bが当たる確率」であれば, 答えは,

上の2つの確率では「a がはずれ, b が当たる」という結果は同じなのですが, 異なる値を求めることになる
ので注意しましょう。
≪① 「aがはずれたときに, bが当たる確率」≫
「aがくじを引いてしまっていて, それがはずれであることがわかっている」
という状況を想像して考えてみましょう。
このときに, bがくじを引いて当たる確率はどうなるか…?と考えると,
aがくじを引いた残りのくじは7本で, そのうち当たりくじが3本あるわけですから,

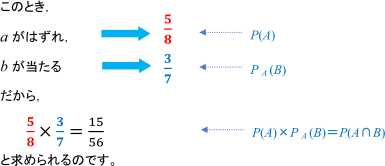
≪② 「aがはずれ、bが当たる確率」≫
一方, 「aがはずれ, bが当たる」という場合は,
「これから, a, bの順にくじを引く場合」を想像してみましょう。
少しややこしいなぁと感じたかもしれませんが, ①と②の違いは, わかりましたか?

【学習アドバイス】
数学の問題は, 日常生活の感覚とは少し異なるときもあり, 慣れないととまどうこともあると思います。問題を
通して, 「こういうときは, こういう確率を求める」ということに慣れて覚えていきましょう。
これからも『進研ゼミ高校講座』の教材を利用していろいろな問題に取り組み, 様々な解法を身につけていき
ましょうね。応援していますよ。
















