数学A 定期テスト対策【場合の数と確率】和の法則と積の法則の使い分けについて

進研ゼミからの回答

こんにちは。
いただいた質問について、早速、回答します。

【質問の確認】

大中小の３つのさいころを投げた時、次のようになる場合は何通りあるか。という問題で

(1）目の積が偶数　　（2）目の和が奇数

このとき和の法則か、積の法則のどちらを使えばよいかについてですね。

【解説】

このような問題は、場合分けをして樹形図をかいて調べるとよいでしょう。

≪(1) 目の積が偶数　の場合≫
を考えてみましょう。
3つのさいころの目の積が偶数のときは、
（ア）　偶×奇×奇　　（イ）　偶×偶×奇　　（ウ）偶×偶×偶
の3つの場合があります。

ところが、さいころには大、中、小の区別があるので、

（ア）偶×奇×奇　の場合
　（大×中×小）＝（偶×奇×奇）、（奇×偶×奇）、（奇×奇×偶）
　の3つのパターンがあります。
（イ）偶×偶×奇　の場合も同様に、
　（大×中×小）＝（偶×偶×奇）、（奇×偶×偶）、（偶×奇×偶）
　の3つのパターンがあります。
（ウ）偶×偶×偶　の場合は
　（大×中×小）＝（偶×偶×偶）　だけですね。

全部で7つのパターンがありますが、それぞれ同時には起こりません。
だから、この7つはそれぞれ和の法則で、加えることになるのです。

次に、その中の1つのパターンを考えてみましょう。
（大×中×小）＝（偶×奇×奇）の場合について
偶数が出るのは、2，4，6の3通り、奇数が出るのは、1，3，5の3通り
であるので、どちらも3通りで考えればよいですね。

大の目が３通り出て、その各々に対して中の目が3通り、またその各々に
対して小の目が3通り出るので、積の法則になります。
よって、（大×中×小）＝（偶×奇×奇）となるのは、3×3×3＝27通り
他のパターンもすべて27通りとなります。

これが7パターンあるから、和の法則で
27＋27＋27＋27＋27＋27＋27＝27×7＝189通り　となるのです。

別解　実は、この問題は余事象の考え方を使うと、ずっと楽に求められます。すべてのさいころの目の出方は6×6×6＝216通りあります。
ここで先に考えた目の組合せ　（ア）、（イ）、（ウ）以外に　（エ）　奇×奇×奇 の場合がありますが、これだけが目の積が奇数になってしまいます。

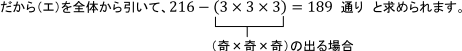
≪(2) 目の和が奇数　の場合≫
（ア）（奇＋奇＋奇）、（イ）（奇＋偶＋偶）のときです。
（イ）は(1)と同じ考え方で、
　（大＋中＋小）＝（偶＋偶＋奇）、（奇＋偶＋偶）、（偶＋奇＋偶）
の3パターンあり、(ア)と合わせて全部で4パターンになります。
これらは同時には起こらないので、和の法則で加えます。

そのうちの1つのパターン（奇＋偶＋偶）の場合は、積の法則で3×3×3＝27通りあり、それが4パターンなので　和の法則より
27+27+27+27=27×4=108通り
となるのです。

【アドバイス】

大の目が出て、中の目が出て、小の目が出ることによって、目の積が偶数になったり、目の和が奇数になったりします。このようなときは「積の法則」です。
一方（奇、奇、奇）の場合と（奇、偶、偶）の場合は同時には起こりません。
このようなときは「和の法則」になります。
「和の法則」と「積の法則」の違いをしっかり理解しておきましょう。

それでは　これからもゼミ教材を活用して力を伸ばしていきましょう。