【場合の数と確率】組分けの問題の見分け方
(2)と(3)の違いがわかりません。
過去の質問の区別の仕方を参照すると(2)は わかりましたが
(3)は本に対しての区別があるので
(2)のやり方だとわかりません。
(3)のStep2の解説もよくわからないので
詳しいわかりやすい、説明をお願いします。
特に、「同じ分け方になる」がわかりません。
進研ゼミからの回答
こんにちは。頑張って勉強に取り組んでいますね。
いただいた質問について、さっそく回答させていただきます。
【質問の確認】
【問題】
異なる9冊の本を次のように分ける方法は何通りあるか。
(2) A君、B君、C君に3冊ずつ分ける。
(3) 3冊ずつ3組に分ける。
(2)と(3)の違いと
【解答解説】
まず、組が区別できるとして分け方を考える方法
A、B、Cの3組に区別できるとすると、3冊ずつ3組に分ける分け方は、(2)より、1680通り。 STEP1
A、B、Cの区別をなくすと、同じ分け方となるものは、 STEP2
A、B、Cの順列の数、つまり、3!通りずつ出てくる。
よって、求める分け方の総数は、
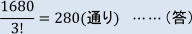
STEP2の解説について
「STEP2の解説もよくわからないので詳しいわかりやすい、説明をお願いします」という質問ですね。
【解説】
(2)と(3)の違いは、3冊ずつ3つに分けた組に区別があるかないかの違いです。
「9冊の中からA君に与える3冊をまず選び、次に残りの6冊からB君に与える3冊を選び、残った3冊をC君に与える」と考えるのが、(2)ですね。
この場合、
A君(①②③)、B君(④⑤⑥)、C君(⑦⑧⑨)
と
A君(④⑤⑥)、B君(⑦⑧⑨)、C君(①②③)
という分け方は、異なる分け方になります。
ところが、誰に与えるかという区別をつけないと、
(①②③)、(④⑤⑥)、(⑦⑧⑨)・・・(ア)
の順に選んだものと
(④⑤⑥)、(⑦⑧⑨)、(①②③)・・・(イ)
の順に選んだものは、どちらも出来上がった3つの組が、
(①②③)と(④⑤⑥)と(⑦⑧⑨)
となり、(ア)、(イ)は、同じものを表します。(選ぶ順番が異なっていても出来上がったものは同じ)
これを「同じ分け方」と表しています。(「分け方としては同じになる」という意味です。)
(3)では、このような「同じ分け方」になるものを1通りと考えたときの分け方の数を求めるのです。
そこで、同じ分け方になるものは何通りあるかと考えると、
例えば、(①②③) と (④⑤⑥) と (⑦⑧⑨) の場合は、
(①②③)、(④⑤⑥)、(⑦⑧⑨)
(①②③)、(⑦⑧⑨)、(④⑤⑥)
(④⑤⑥)、(⑦⑧⑨)、(①②③)
(④⑤⑥)、(①②③)、(⑦⑧⑨)
(⑦⑧⑨)、(①②③)、(④⑤⑥)
(⑦⑧⑨)、(④⑤⑥)、(①②③)
の6通りとなります。
つまり、(2)では6通りと考えたものが、(3)では1通りとなるのです。
よって、(3)では、(2)で求めた場合の数を同じ分け方となる数(A、B、Cの順列の数)で割っているのです。
【アドバイス】
いくつかのものを何組かに分ける方法の数を求めるには、組合せの考え方を1組ずつ順番に使って求めていきます。
その際、区別できない組があるときには、
STEP1 組に区別がつくものとして、場合の数を求める。
STEP2 組の区別をなくしたとき、何通りの同じ分け方があるか求める。
STEP3 STEP1で求めた場合の数をSTEP2で求めた数で割る。
と考えていきます。
いろいろな問題を解いていくと、問題のどの部分に注目して考えていけばよいのか判断できるようになります。
「チャレンジ」の問題などを利用して練習していきましょう。
それではこれで回答を終わります。これからも『進研ゼミ高校講座』を活用して学習を進めていってくださいね。
















