【1次関数】 「図形の辺上を動く点」の変域の求め方
![[問題]点PはAを出発し、図のような長方形の長さの辺上をB、Cを通ってDまで動く。点Pが毎秒2cmの速さで動くとき、Aを出発してからの時間をx秒とする。このときのxの変域の考え方がわかりません。](/teikitest/_resource/img/chu/math/c_m_338_1.png)
進研ゼミからの回答
辺ごとに場合分けして考えるのがこの問題のポイントです。
点Pが,①AB上を動くとき,②BC上を動くとき,③CD上を動くときの3つに分けられます。
(時間)は(動いた長さ)÷(速さ)で求められるので,AからBまで2秒,BからCまで3秒,CからDまで2秒かかります。
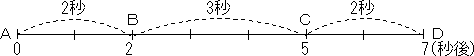
それぞれの変域を不等号で表すと次のようになります。
①0≦x≦2 ②2≦x≦5 ③5≦x≦7
![[問題]点PはAを出発し、図のような長方形の長さの辺上をB、Cを通ってDまで動く。点Pが毎秒2cmの速さで動くとき、Aを出発してからの時間をx秒とする。このときのxの変域の考え方がわかりません。](/teikitest/_resource/img/chu/math/c_m_338_1.png)
辺ごとに場合分けして考えるのがこの問題のポイントです。
点Pが,①AB上を動くとき,②BC上を動くとき,③CD上を動くときの3つに分けられます。
(時間)は(動いた長さ)÷(速さ)で求められるので,AからBまで2秒,BからCまで3秒,CからDまで2秒かかります。
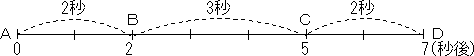
それぞれの変域を不等号で表すと次のようになります。
①0≦x≦2 ②2≦x≦5 ③5≦x≦7
※このQ&Aでは、 「進研ゼミ中学講座」会員から寄せられた質問とその回答の一部を公開しています。
Q&Aをすべて見る(「進研ゼミ中学講座」会員限定)